Let A=[1tanx−tanx1]&B=ATA−2 if f(x)=det(adjB) then number of solution(s) of the equation 10f(x)–x=0 is (are)
[Note: det(P) denotes the determinant of a square matrix P]
The correct Answer is:7.00
f(x)=det(adj)(B))=|adj(B)|=|B|
=∣∣AT∣∣∣∣A−2∣∣=|A|1|A|2
=1|A|=1sec2x=cos2x
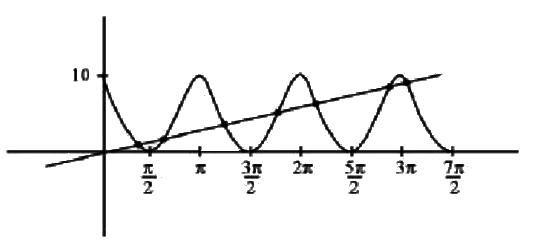
10cos2x−x=0
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(x)=max{tanx,cotx}. Then the number of roots of the equation f(x)=12 in (0,2π) is
A0B1C2D4 - Question 2 - Select One
Let A = [x+23x3x+2],B=[x05x+2]. Then all solutions of the equation det (AB ) = 0 is
A1, - 1, 0, 2B1, 4, 0, -2C1, - 1, 4, 3D−1,4,0,3 - Question 3 - Select One
Let matrix A=⎡⎢⎣xy−z123112⎤⎥⎦ where x,y,z∈N. If det. (adj. (adj. A))=28⋅34 then the number of such matrices A is :
[Note : adj. A denotes adjoint of square matrix A.]A220B45C55D110
Let f(x)=max{tanx,cotx}. Then number of roots of the equation f(x)=1√3∈(0,2π) is (A) 2 (B) 4 (C) 0 (D) infinite
View SolutionLet B be a skew symmetric matrix of order 3×3 with real entries. Given I−B and I+B are non-singular matrices. If A=(I+B)(I−B)−1, where det(A)>0 ,then find the value of det(2A)−det(adj(A)) [Note: det(P) denotes determinant of square matrix P and det(adj(P)) denotes determinant of adjoint of square matrix P respectively.]
View SolutionLet A = ⎡⎢⎣−120315−12−1⎤⎥⎦ then det (110adj(adjA))= ______
View SolutionLetf(x)=max{tanx,cotx] then number of roots of equation the interval [0,2π] satisfying f(x)=1√3 is (A) 2(B) 4(C) 0 (D) infinte
View SolutionIf f(x)=x3−12x+p,p∈{1,2,3,…,15} and for each 'p', the number of real roots of equation f(x)=0 is denoted by θ, the 15∑θ is equal to ……….. .
View Solution

