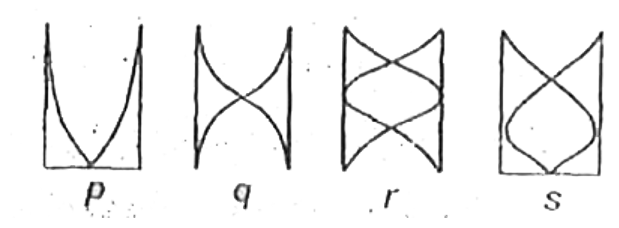The vibrations of four air columns are represented in the adjoining figures. The ratio of frequencies np:nq:nr:ns is
12 : 6 : 3 : 4
1 : 2 : 4 : 3
4 : 2 : 3 : 1
6 : 2 : 3 : 4
The correct Answer is:B
np=V4L,nq=V2L
nr=2V2L,ns=3V4L
∴np:nq:nr:ns=1:2:4:3
Topper's Solved these Questions
Similar Questions
Knowledge Check
Figures shows the vibrations of foue air columns. The ratio of frequencies np:nq:nr:ns is
 A12:3:3:4B1:2:4:3C4:2:3:1D4:3:2:1
A12:3:3:4B1:2:4:3C4:2:3:1D4:3:2:1The frequency of vibration of air column in a pipe closed at one end is n1and that of the one closed at both end is n2. When both the pipes are joined to form a pipe closed atone end, the frequency of vibration of air column in it is (neglecting end correction )
An1n22n2+n1B2n1−n2n1+n2Cn1n22n1+n2Dn1+n2nn−n2Two vibrating strings of the same material but lengths L and 2L have radii 2r and r respectively. They are stretched under the same tension. Both the strings vibrate in their fundamental modes, the one of length L with frequency n1 and the other with frequency n2 the ratio n1/n2 is given by
A2B4C8D1
(nPrnCr)=
View SolutionProve analytically that in the case of a closed organ pipe of length L the frequencies of the vibrating air column are given by v=(2n+1)(v/4L), where n is an integer.
View SolutionProve analytically that in the case of a closed organ pipe of length I, the frequencies of the vibrating air column are given by ν=(2n+1)(v/4L), where n is an integer.
View SolutionA string A has double the length, double the tension, double the diameter and double the density as another string B. Their fundamental frequencies of vibration are nA and nB respectively. The ratio nA/nB is equal to
View SolutionA sonometer wire when vibrated in full length has frequency n. Now, it is divided by the help of bridges into a number of segments of lenths l1,l2,l3… when vibration these segments have frequencies n1,n2,n3,,, Then, the correct relation is
View Solution