Which could be the graph of y=x2+3x+k , where k is an integer ?
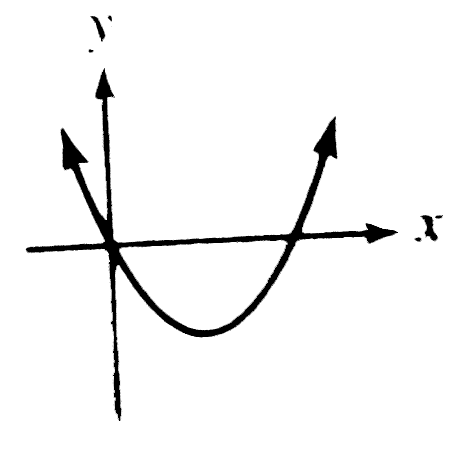
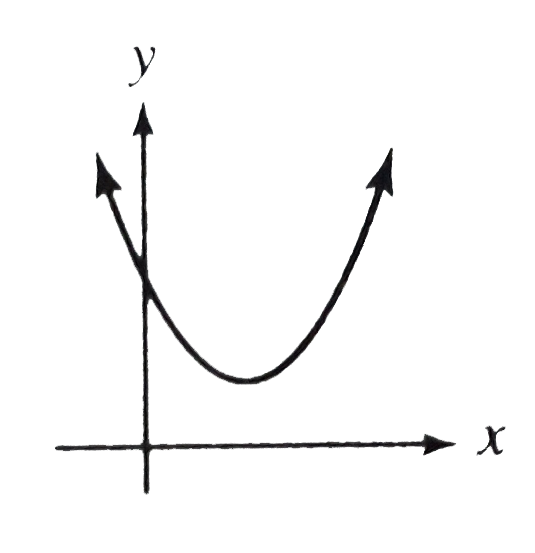
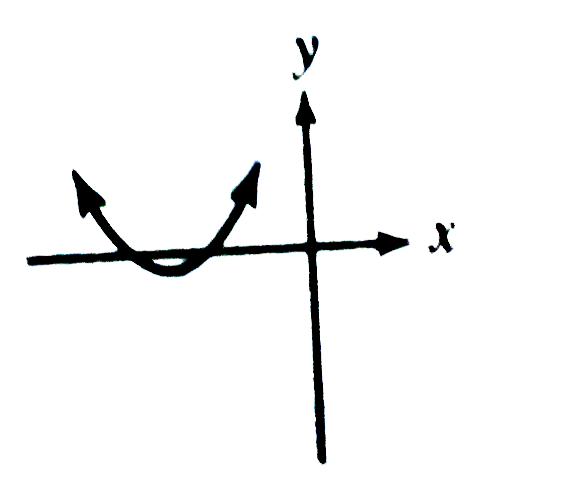

The correct Answer is:C
To determine which graph could represent the equation y=x2+3x+k, where k is an integer, we can follow these steps:
Step 1: Identify the Type of Graph
The equation y=x2+3x+k is a quadratic equation in the standard form y=ax2+bx+c. Here, a=1, b=3, and c=k.
Step 2: Determine the Direction of the Parabola
Since a=1 (which is greater than 0), the parabola opens upwards. This means that any graph option that shows a downward-opening parabola can be eliminated.
Hint: Remember that the sign of a determines the direction of the parabola. If a>0, it opens upwards; if a<0, it opens downwards.
Step 3: Find the Vertex of the Parabola
The x-coordinate of the vertex of a parabola given by y=ax2+bx+c can be calculated using the formula:
x=−b2a
Substituting a=1 and b=3:
x=−32⋅1=−32
Step 4: Analyze the Vertex Position
The x-coordinate of the vertex is −32, which is negative. This means that the vertex lies in the second quadrant (where x is negative).
Hint: The vertex's x-coordinate gives us information about the graph's position. Look for options where the vertex is located in the second quadrant.
Step 5: Evaluate the Graph Options
Now, we can evaluate the given graph options:
- Option A: If the vertex is in the first quadrant (x positive), eliminate this option.
- Option B: If the vertex is also in the first quadrant, eliminate this option.
- Option C: If the vertex is in the second quadrant (x negative), this option remains.
- Option D: If the vertex is in the third quadrant (x negative but opens downwards), eliminate this option.
Conclusion
After evaluating the options, we find that Option C is the only graph that matches the criteria of having an upward-opening parabola with a vertex at x=−32.
Final Answer: The graph of y=x2+3x+k where k is an integer could be represented by Option C.
The equation y=x2+3x+k is a quadratic equation in the standard form y=ax2+bx+c. Here, a=1, b=3, and c=k.
Since a=1 (which is greater than 0), the parabola opens upwards. This means that any graph option that shows a downward-opening parabola can be eliminated.
The x-coordinate of the vertex of a parabola given by y=ax2+bx+c can be calculated using the formula:
x=−b2a
Substituting a=1 and b=3:
x=−32⋅1=−32
The x-coordinate of the vertex is −32, which is negative. This means that the vertex lies in the second quadrant (where x is negative).
Now, we can evaluate the given graph options:
- Option A: If the vertex is in the first quadrant (x positive), eliminate this option.
- Option B: If the vertex is also in the first quadrant, eliminate this option.
- Option C: If the vertex is in the second quadrant (x negative), this option remains.
- Option D: If the vertex is in the third quadrant (x negative but opens downwards), eliminate this option.
After evaluating the options, we find that Option C is the only graph that matches the criteria of having an upward-opening parabola with a vertex at x=−32.
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following translations of the graph of y=x2 would result in the graph of y=x2−6x+k , where k is a constant greater than 10 ?
Aleft 6 units and up k unitsBleft 3 units and up k + 9 unitsCright 3 units and up k + 9 unitsDright 3 units and up k−9 units - Question 2 - Select One
Which of the following could be the graph of y=3−2x ?
A B
B C
C D
D
- Question 3 - Select One
f (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?A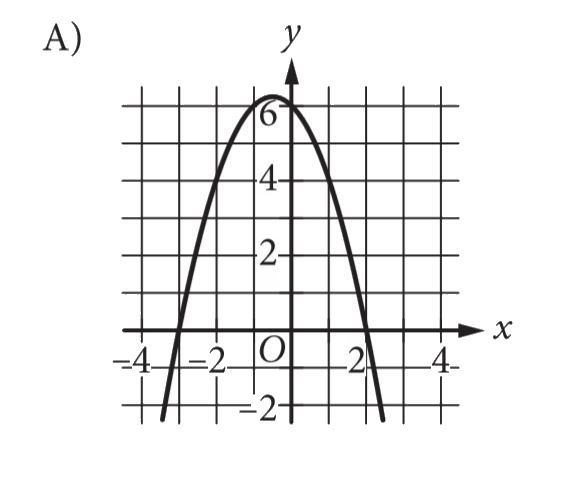 B
B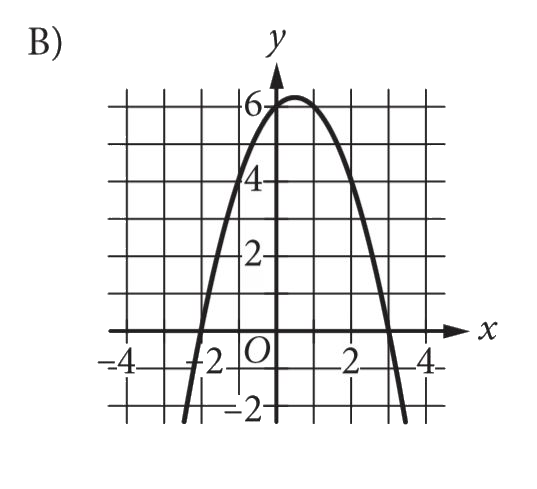 C
C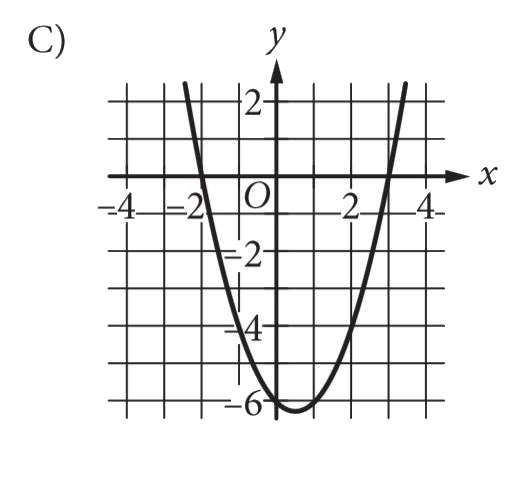 D
D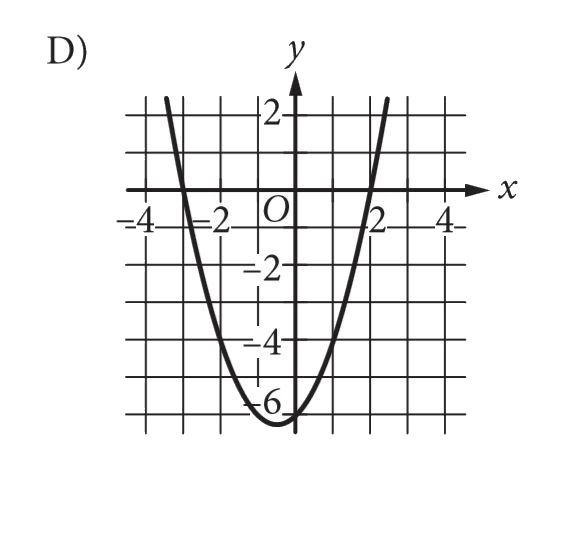
Draw the graph of |y|=[x], where [.] represents the greatest integer function.
View SolutionIn the xy-plane the point (2,5) lies on the graph of the function f. IF f(x) =k−x2 where k is a constant, what is the value of k?
View SolutionDraw the graph of y=[4−x2],|x|≤2, where [.] represents the greatest integer function.
View SolutionWhich of the following could be the graph of 2x+3y+12=0 ?
View SolutionWhich of the following could be the graph of 2x+3y+12=0 ?
View Solution

