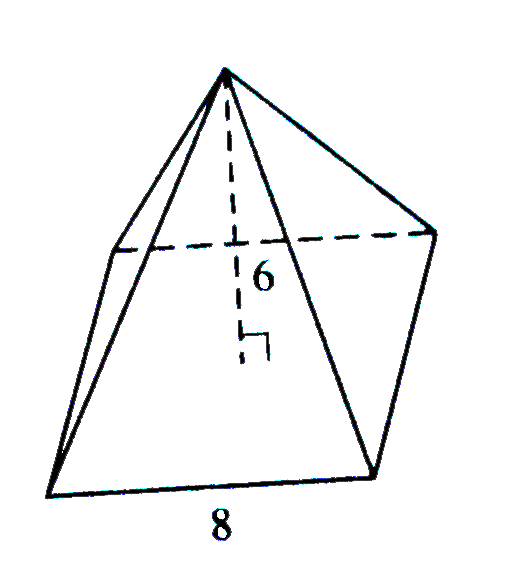
The square pyramid shown above has altitude 6 and side of square base equal to 8. What is the area of one of the triangular faces of the pyramid ?
8√13
16√3
24
40
The correct Answer is:A
Step by step video, text & image solution for The square pyramid shown above has altitude 6 and side of square base equal to 8. What is the area of one of the triangular faces of the pyramid ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST24videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - 1600 CLUB BACKGROUND TOPICSEXERCISE - PRACTICE TEST11videos
1600 CLUB BACKGROUND TOPICS
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE45videos
ADDITIONAL TOPICS IN MATH
Similar Questions
Knowledge Check
- Question 1 - Select One
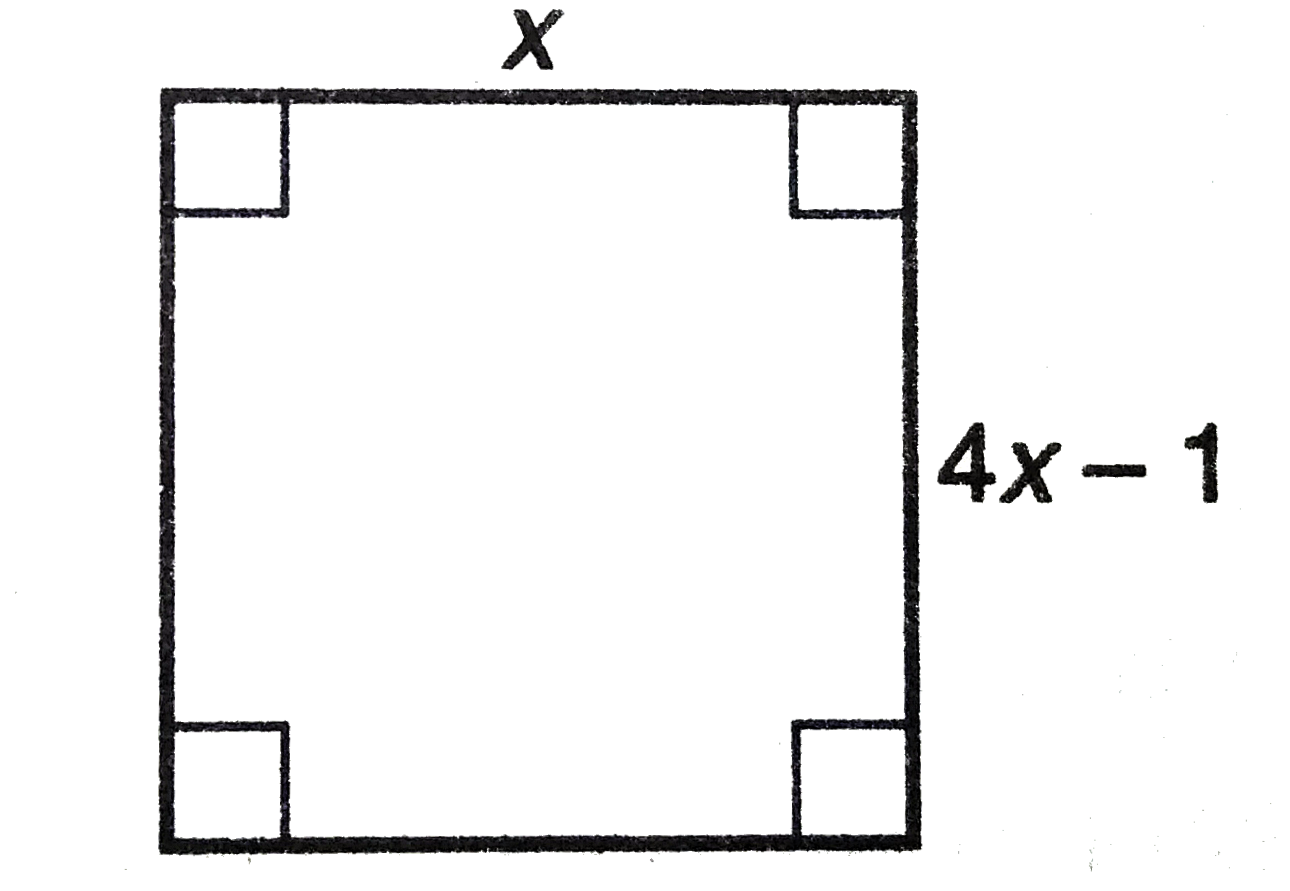
Find the surface area of a cube if the area of one of the square faces is 16.
A256B76C72D96 - Question 2 - Select One
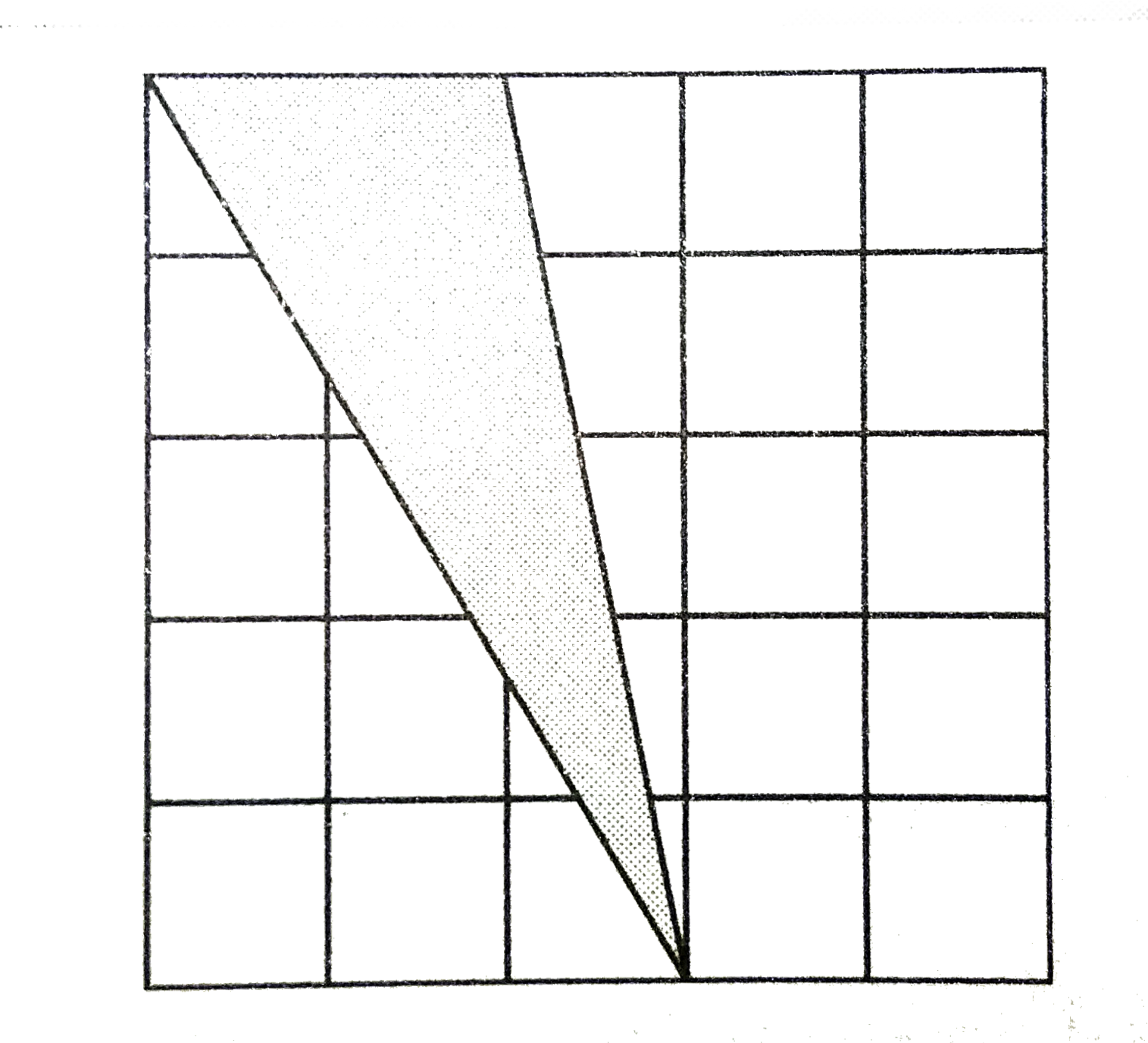
Each of the small squares in the figure above has an area of 4. If the shortest , what is the area of the shaded triangle?A40B24C20D16 - Question 3 - Select One
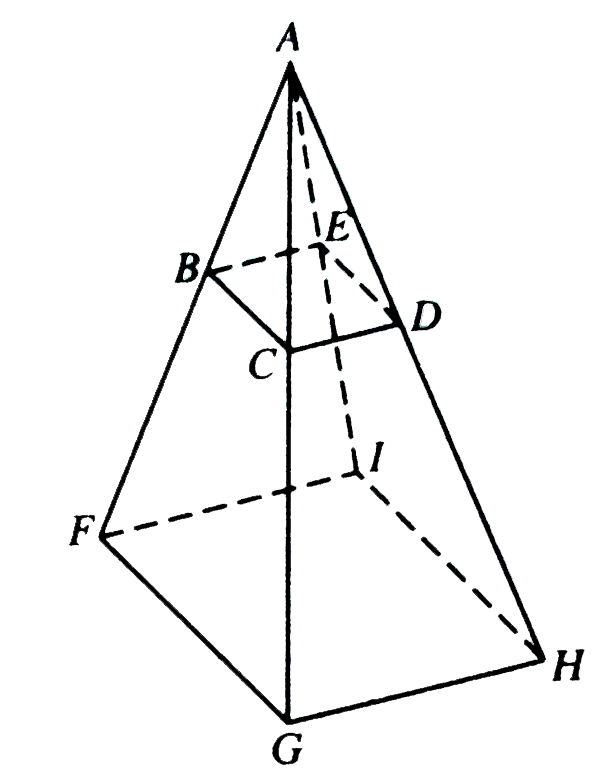
The pyramid in the figure above has square base FGHI , and all triangular faces are congruent. The base BCDE of the small pyramid is also square , and is parallel to FGHI. If the ratio of the area of square BCDE to the area of square FGHI is 1:4 , what is the ratio of the volume of the small pyramid to the volume of the large pyramid ?A1:2B1:3C1:4D1:8
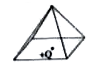
A point charge is positioned at the centre of the base of a square pyramid as shown. The flux through one of the four identical upper faces of the pyramid is, qPε0 then P is
 View Solution
View SolutionWhat is the area of a square whose sides are doubled?
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionIn an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
View Solution