Joe was asked to fill up the missing digits A and B in the number 25A7B subject to the condition that the resulting number has to be divisible by 36.What is the value of (A + B) if A and B are distinct digits ?
4
8
9
13
The correct Answer is:D
To solve the problem of finding the missing digits A and B in the number 25A7B such that the number is divisible by 36, we need to follow these steps:
Step 1: Understand the conditions for divisibility by 36
A number is divisible by 36 if it is divisible by both 4 and 9.
Step 2: Check divisibility by 4
For a number to be divisible by 4, the last two digits must form a number that is divisible by 4. In our case, the last two digits are 7B.
- The possible values for B (0-9) will give us the following two-digit numbers:
- 70, 71, 72, 73, 74, 75, 76, 77, 78, 79.
- Among these, the numbers divisible by 4 are:
- 72 (7B = 72, B = 2)
- 76 (7B = 76, B = 6)
Thus, B can be either 2 or 6.
Step 3: Check divisibility by 9
For a number to be divisible by 9, the sum of its digits must be divisible by 9. The sum of the digits in 25A7B is:
2+5+A+7+B=14+A+B
We need to check the cases for B = 2 and B = 6.
Case 1: B = 2
Substituting B = 2 into the sum:
14+A+2=16+A
We need this to be divisible by 9. The possible values of 16+A that are divisible by 9 are:
- 18 (which gives A = 2)
- 27 (which gives A = 11, not possible since A must be a single digit)
Since A = 2 is not distinct from B, we discard this case.
Case 2: B = 6
Substituting B = 6 into the sum:
14+A+6=20+A
We need this to be divisible by 9. The possible values of 20+A that are divisible by 9 are:
- 27 (which gives A = 7)
- 36 (which gives A = 16, not possible since A must be a single digit)
In this case, A = 7 is distinct from B = 6.
Step 4: Calculate A + B
Now that we have found A = 7 and B = 6, we can calculate:
A+B=7+6=13
Final Answer
The value of A+B is 13.
---
A number is divisible by 36 if it is divisible by both 4 and 9.
For a number to be divisible by 4, the last two digits must form a number that is divisible by 4. In our case, the last two digits are 7B.
- 70, 71, 72, 73, 74, 75, 76, 77, 78, 79.
- Among these, the numbers divisible by 4 are:
- 72 (7B = 72, B = 2)
- 76 (7B = 76, B = 6)
For a number to be divisible by 9, the sum of its digits must be divisible by 9. The sum of the digits in 25A7B is:
2+5+A+7+B=14+A+B
Substituting B = 2 into the sum:
14+A+2=16+A
We need this to be divisible by 9. The possible values of 16+A that are divisible by 9 are:
- 18 (which gives A = 2)
- 27 (which gives A = 11, not possible since A must be a single digit)
Substituting B = 6 into the sum:
14+A+6=20+A
We need this to be divisible by 9. The possible values of 20+A that are divisible by 9 are:
- 27 (which gives A = 7)
- 36 (which gives A = 16, not possible since A must be a single digit)
Now that we have found A = 7 and B = 6, we can calculate:
A+B=7+6=13
The value of A+B is 13.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
AB denotes a two -digits number with digits as A and B. If (AB)2=ACC, where ACC denotes a three - digits number having digits A,C and C. What is the value of A+ B + C if A,B,C are all distinct digits?
A5B6C7D9 - Question 2 - Select One
AB and CA are two -digit numbers which satisfy the multiplication:
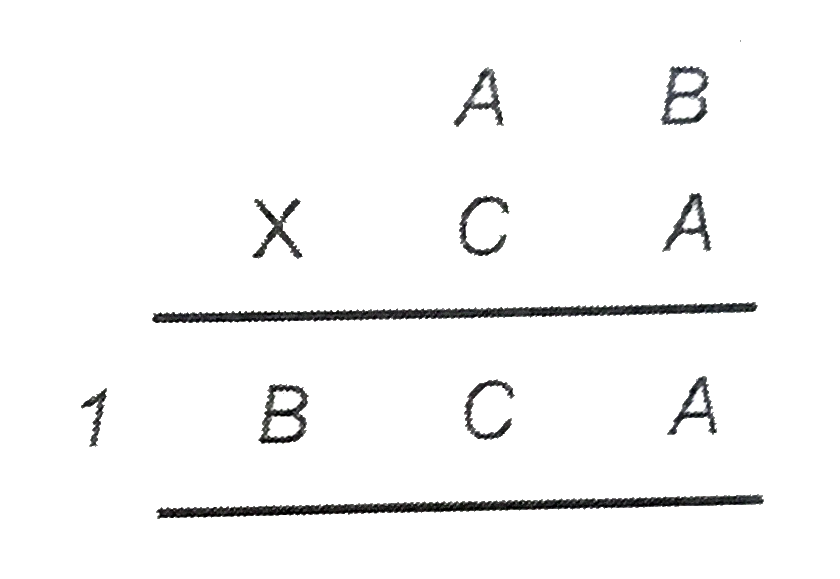
If A,B,C are distinct integers from 2 to 5 , what is the value of A + B + C?A2B3C5D10
If a 679b is a five digit number that is divisible by 72, then a+b is equal to
View SolutionIf a is an irrational number which is divisible by b, then the number b
View SolutionGiven that the number 59142a is divisible by 4, where a is a digit, what are the possible values of a ?
View SolutionWrite the smallest digit and the greatest digit in the blank space of each of the followingnumbers so that the number formed is divisible by 3 :(a) (b)
View SolutionGiven that the number 60ab57377 is divisible by 99, where a and b are digits, what are the values of a and b ?
View SolutionThe number 3 divides a with a result of b and a remainder of 2. The number 3 divides b with a result of 2 and a remainder of 1. What is the value of a?
View Solution

