The distance ,d, in feet covered by a ball in the nth second after being dropped from the top of a building is given by d=6n+1 . What is the total distance , in feet covered by the ball in the first 5 seconds ?
27
31
65
95
To find the total distance covered by the ball in the first 5 seconds, we will use the formula given in the question:
d=6n+1
where d is the distance covered in the nth second.
1. Calculate the distance covered in the 1st second (n = 1):
d1=6(1)+1=6+1=7 feet
2. Calculate the distance covered in the 2nd second (n = 2):
d2=6(2)+1=12+1=13 feet
3. Calculate the distance covered in the 3rd second (n = 3):
d3=6(3)+1=18+1=19 feet
4. Calculate the distance covered in the 4th second (n = 4):
d4=6(4)+1=24+1=25 feet
5. Calculate the distance covered in the 5th second (n = 5):
d5=6(5)+1=30+1=31 feet
6. Sum the distances covered in the first 5 seconds:
Total distance=d1+d2+d3+d4+d5
Total distance=7+13+19+25+31
7. Calculate the total:
Total distance=7+13=20
20+19=39
39+25=64
64+31=95
Thus, the total distance covered by the ball in the first 5 seconds is 95 feet.
Final Answer:
The ball covers a total distance of 95 feet in the first 5 seconds.
---
d1=6(1)+1=6+1=7 feet
d2=6(2)+1=12+1=13 feet
d3=6(3)+1=18+1=19 feet
d4=6(4)+1=24+1=25 feet
d5=6(5)+1=30+1=31 feet
Total distance=d1+d2+d3+d4+d5
Total distance=7+13+19+25+31
Total distance=7+13=20
20+19=39
39+25=64
64+31=95
The ball covers a total distance of 95 feet in the first 5 seconds.
Similar Questions
A ball dropped from the top of a building takes 0.5 sec to clear the window of 4.9 m height. What is the height of building above the window?
View SolutionMoving with a uniform acceleration from the state of rest a body covers 22 m during the 6th sec of its motion. What is the distance covered by if during the first 6 sec?
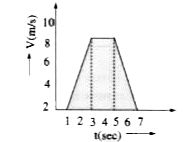
View SolutionFor the velocity - time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the total distance covered by it in all the seven seconds
View SolutionA particle is dropped from the top of a tower. Its covered distance in last 1 sec is equal to distance covered by particle in 1st3s. Find height of tower.
View SolutionA particle is dropped from the top of a high building 360 m. The distance travelled by the particle in ninth second is (g=10m/s2)
View SolutionFor a stone what is the ratio of the distance covered in its 1st, 3rd and 5th seconds of its free fall.
View SolutionThe height h , in feet , of a ball shot upward from a ground level spring gun is described by the formula h=−16t2+48t. Where t is the time in seconds. What is the maximum height , in feet , reached by the ball ?
View SolutionA ball is dropped downwards . After 1 second another ball is dropped downwards from the same point . What is the distance between them after 3 seconds .
View SolutionA ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View SolutionA ball is dropped from the top of a tower of herght (h). It covers a destance of h//2 in the last second of its motion. How long does the ball remain in air?
View Solution
