f(x)=x2+16. For what value of k is f(2k+1)=2f(k)+1 if k is a positive integer?
The correct Answer is:2
To solve the equation f(2k+1)=2f(k)+1 for the function f(x)=x2+16, we will follow these steps:
Step 1: Find f(2k+1)
We start by substituting 2k+1 into the function f(x).
f(2k+1)=(2k+1)2+16
Expanding (2k+1)2:
(2k+1)2=4k2+4k+1
Thus,
f(2k+1)=4k2+4k+1+16=4k2+4k+17
Step 2: Find 2f(k)+1
Next, we calculate f(k) and then find 2f(k)+1.
f(k)=k2+16
Now, multiplying by 2 and adding 1:
2f(k)=2(k2+16)=2k2+32
Thus,
2f(k)+1=2k2+32+1=2k2+33
Step 3: Set the two expressions equal to each other
Now we set f(2k+1) equal to 2f(k)+1:
4k2+4k+17=2k2+33
Step 4: Rearrange the equation
We can rearrange this equation to bring all terms to one side:
4k2+4k+17−2k2−33=0
This simplifies to:
2k2+4k−16=0
Step 5: Simplify the equation
Dividing the entire equation by 2 gives:
k2+2k−8=0
Step 6: Factor the quadratic equation
Now we factor the quadratic equation:
(k−2)(k+4)=0
Step 7: Solve for k
Setting each factor to zero gives us:
k−2=0⇒k=2
k+4=0⇒k=−4
Since we are looking for the positive integer value of k, we find:
k=2
Final Answer
The value of k is 2.
---
We start by substituting 2k+1 into the function f(x).
Next, we calculate f(k) and then find 2f(k)+1.
Now we set f(2k+1) equal to 2f(k)+1:
We can rearrange this equation to bring all terms to one side:
Dividing the entire equation by 2 gives:
Now we factor the quadratic equation:
Setting each factor to zero gives us:
k+4=0⇒k=−4
The value of k is 2.
Topper's Solved these Questions
Similar Questions
The function f(x) is defined as follows:
f(x)=x2−1ifx≤3f(x)=2x+2if3<x≤9f(x)=4x−8ifx>9
What is the value of k if f(f(f(3)))=(k+1)2 where k is positive integer ?
View SolutionIf N denotes the set of all positive integers and if f:N→N is defined by f(n)= the sum of positive divisors of n then f(2k⋅3), where k is a positive integer is
View Solution
Knowledge Check
For what value of k, then function f(x) = k(x + sin x) + k is increasing ?
Ak = -1Bk<−1Ck>0Dk<0f (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?A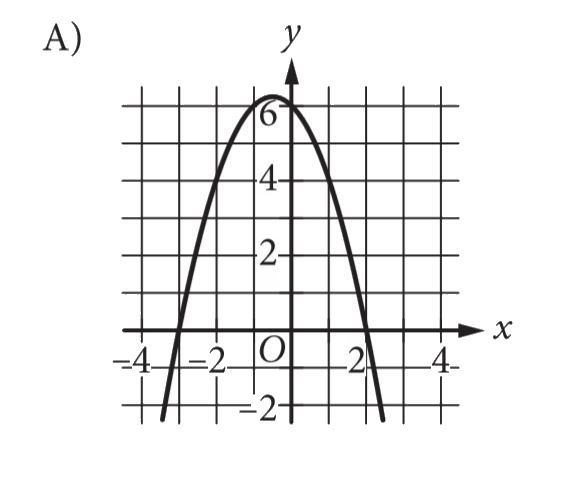 B
B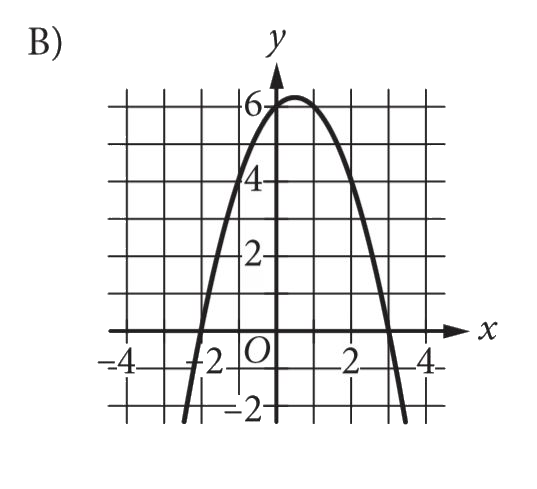 C
C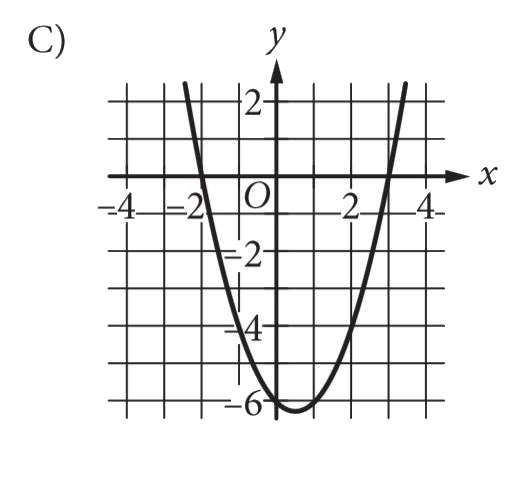 D
D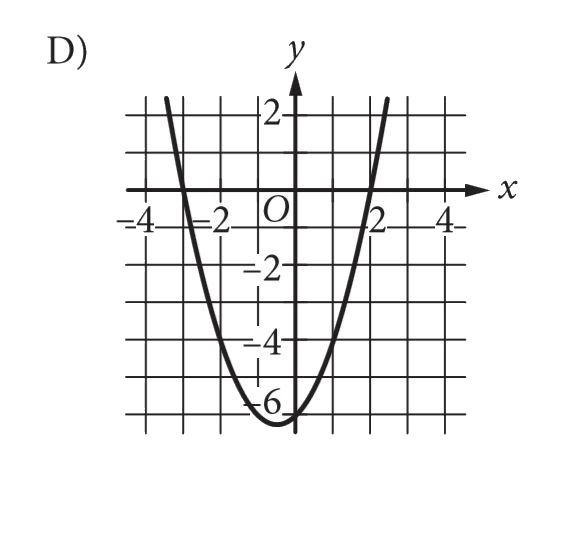

The graph of f(x) and g(x) are shown below. If 3f(g(k)+1)+g(f(m)), where k and m are positive integers from 1 to 5, what is the maximum value of (K+m)?
View SolutionIf A=[3−41−1] prove that Ak=[1+2k−4kk1−2k] where k is any positive integer.
View SolutionThe least integral value of 'k' If (k−1)x2−(k+1)x+(k+1) is positive for all real value of x is:
View SolutionLet f(x)=a2kx2k+a2k−1x2k−1+...+a1x+a0b2kx2k+b2k−1x2k−1+...+b1x+b0, where k is a positive integer, ai,bi∈R and a2k≠0,b2k≠0 such that b2kx2k+b2k−1x2k−1+...+b1x+b0=0 has no real roots, then
View SolutionFor what value of k is the function f(x)={x2−1x−1, x≠1k, x=1 continuous at x=1 ?
View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:
View Solution
