An object detected or radar is 5 miles to the east, 4 miles to the north, and 1 mile above the tracking station. Among the following, which is the closet approximation to the distance, in miles, that the object is from the tracking station?
6.5
7.2
8.3
9.0
The correct Answer is:A
To find the distance from the tracking station to the object detected by radar, we can use the Pythagorean theorem in a three-dimensional context. Here’s the step-by-step solution:
Step 1: Identify the coordinates
The tracking station is at the origin point (0, 0, 0). The object is located:
- 5 miles to the east (x-axis)
- 4 miles to the north (y-axis)
- 1 mile above (z-axis)
Thus, the coordinates of the object are (5, 4, 1).
Step 2: Calculate the distance in the horizontal plane
First, we need to find the distance from the tracking station to the projection of the object in the horizontal plane (ignoring the height). This forms a right triangle where:
- One leg (east) = 5 miles
- Another leg (north) = 4 miles
Using the Pythagorean theorem:
dhorizontal=√(52)+(42)=√25+16=√41
Step 3: Calculate the total distance
Now we need to find the distance from the tracking station to the object in three dimensions. We treat the distance we just calculated as one leg of a new right triangle where:
- One leg = dhorizontal=√41
- The other leg (height) = 1 mile
Using the Pythagorean theorem again:
dtotal=√(√41)2+(12)=√41+1=√42
Step 4: Approximate the distance
Now we need to approximate √42:
√42≈6.48
Thus, the distance from the tracking station to the object is approximately 6.48 miles.
Step 5: Final answer
The closest approximation to the distance in miles that the object is from the tracking station is 6.5 miles.
---
The tracking station is at the origin point (0, 0, 0). The object is located:
- 5 miles to the east (x-axis)
- 4 miles to the north (y-axis)
- 1 mile above (z-axis)
First, we need to find the distance from the tracking station to the projection of the object in the horizontal plane (ignoring the height). This forms a right triangle where:
- One leg (east) = 5 miles
- Another leg (north) = 4 miles
dhorizontal=√(52)+(42)=√25+16=√41
Now we need to find the distance from the tracking station to the object in three dimensions. We treat the distance we just calculated as one leg of a new right triangle where:
- One leg = dhorizontal=√41
- The other leg (height) = 1 mile
dtotal=√(√41)2+(12)=√41+1=√42
Now we need to approximate √42:
√42≈6.48
The closest approximation to the distance in miles that the object is from the tracking station is 6.5 miles.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - IMPROVING YOUR MATH SCOREEXERCISE - BASIC MATH PROBLEMS IN SETTINGS6videos
IMPROVING YOUR MATH SCORE
- BOOK - ENGLISH SATCHAPTER - HIGHER DEGREE POLYNOMIALS EXERCISE - EXERCISES6videos
HIGHER DEGREE POLYNOMIALS
- BOOK - ENGLISH SATCHAPTER - INTERMEDIATE ALGEBRA/COORDINATE GEOMETRYEXERCISE - EXERCISE12videos
INTERMEDIATE ALGEBRA/COORDINATE GEOMETRY
Similar Questions
A straight road is at a distance of 5√2 miles from a place. The shortest distance of the road from the place is in the N.E. direction. Do the following villages which (i) is 6 miles East and 4 miles North from the place lie on the road or no, (ii) is 4 miles East and 3 miles North from the place, lie on the road or not?
View SolutionThe earth is made up of four primary layers: the inner core, outer core, mantle, and crust.The outer core is more than 800 miles and less than 2,200 miles from the Earth's center. Which of the following inequalities represents all possible distances, d, in miles, from the Earth's center that are in the outer core?
View Solution
Knowledge Check
- Question 1 - Select One
A cargo ship is 4.2 miles from a lighthouse, and a fishing boat is 5.0 miles from the lighthouse, as shown below. The angle between the straight lines from the lighthouse to the 3 vessels is 5∘. The approximate distance in miles, from the cargo ship to the fishing boat is given by which of the following expressions?
(Note: The law of cosines states that for any triangle with vertices A, B and C adn the sides opposite those vertices with length a, b, and c, respectively. c2=a2+b2−2abcosC).
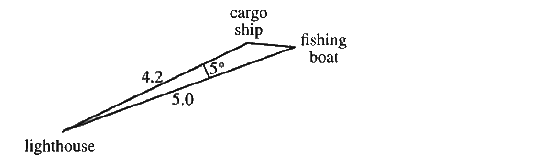 A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘
A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘ - Question 2 - Select One
In the figure below, a highway rest area (at D) and radar stations (at A and B) lie on a level east-west line, A is 9,000 feet due west of D. An airplane (at C) is shown directly above the rest area, flying due west at a constant speed of 300 feet per secod and at a constant altitude of 12,000 feet. The airplane is located at a straight-line distance of 15,000 feet from the radar station at A and 13,000 feet from the radar station at B.
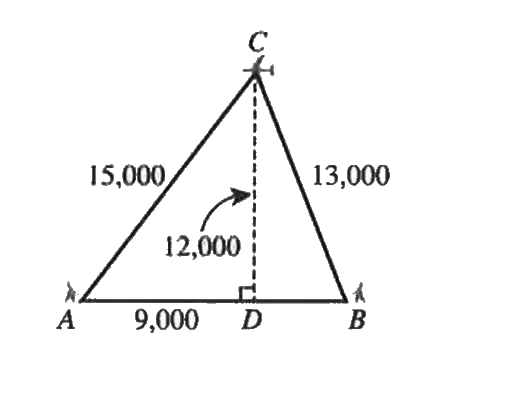
Which of the following values is closest to the distance, in feet, between the 2 radar stations?A5,000B10000C145000D15000 - Question 3 - Select One
Katie hikes 5 miles north, 7 miles east, and then 3 miles north again. What number of miles, measured in a straight line, is katie from her starting point?
A√83B10C√113D13
The distance traveled by Earth in one orbit around the Sun is about 580,000,000 miles. Earth makes one complete orbit around the Sun in one year. Of the following, which is closest to the average speed of Earth, in miles per hour, as it orbits the Sun?
View SolutionOn the certain map, 1.5 inches represents a distance of 120 miles. If two cities on this map are 1 foot apart, what is the distance, in miles, between the cities?
View SolutionDuring a comping trip. Aundria and Annette decide to travel to their campsite using two different routes. Aundria takes the hiking trail that travels 5 miles south, 6 miles east, 7 miles south, and 2 miles west to the campsite, Annette uses the cross-country route that starts at the same point as the kiking trail but goes in a straight line from there to the campsite. About how many miles total will the two travel?
View SolutionChris can run 3.6 miles in 44 minutes. If the continues to run at this pace, which of the following is closest to the distance he will travel in 3 hours?
View SolutionIn the figure below, a highway rest area (at D) and radar stations (at A and B) lie on a level east-west line, A is 9,000 feet due west of D. An airplane (at C) is shown directly above the rest area, flying due west at a constant speed of 300 feet per secod and at a constant altitude of 12,000 feet. The airplane is located at a straight-line distance of 15,000 feet from the radar station at A and 13,000 feet from the radar station at B.
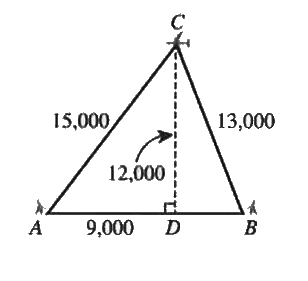
Which of the following values is closest to the number of seconds it will take for the airplane to fly from C to the point directly above the radar station at A?View Solution

