A line contains the points A,B,C and D. Point B is between points A and C. Point D is between points C and B. Which of the following inequalities must be true about lengths of these segments?
BC lt AB
BD lt AB
BD lt CD
CD lt BC
The correct Answer is:D
To solve the problem, we need to analyze the positions of points A, B, C, and D on a line and determine which inequalities must be true based on their relative positions.
1. Understanding the Positioning of Points:
- We know that point B is between points A and C. This means that the order of points on the line is A, B, C.
- Point D is between points C and B. This means that the order of points on the line is C, D, B.
2. Visual Representation:
- We can represent the points on a number line for clarity:
A−−−−B−−−−C∣D
- Here, D is positioned between C and B.
3. Identifying the Lengths:
- Let's denote the lengths of segments as follows:
- Length of segment AB = |AB|
- Length of segment BC = |BC|
- Length of segment CD = |CD|
- Length of segment BD = |BD|
4. Analyzing the Inequalities:
- Since D is between C and B, we can conclude that:
- The length of segment CD (|CD|) must be less than the length of segment BC (|BC|) because D is a point that lies within the segment BC.
- Therefore, we can express this as:
\(
|CD| < |BC|
\)
5. Conclusion:
- The only inequality that must be true based on the positions of points A, B, C, and D is:
\(
CD < BC
\)
- Hence, the correct answer is that the inequality \( CD < BC \) must always hold true.
- We know that point B is between points A and C. This means that the order of points on the line is A, B, C.
- Point D is between points C and B. This means that the order of points on the line is C, D, B.
- We can represent the points on a number line for clarity:
A−−−−B−−−−C∣D
- Here, D is positioned between C and B.
- Let's denote the lengths of segments as follows:
- Length of segment AB = |AB|
- Length of segment BC = |BC|
- Length of segment CD = |CD|
- Length of segment BD = |BD|
- Since D is between C and B, we can conclude that:
- The length of segment CD (|CD|) must be less than the length of segment BC (|BC|) because D is a point that lies within the segment BC.
- Therefore, we can express this as:
\(
|CD| < |BC|
\)
- The only inequality that must be true based on the positions of points A, B, C, and D is:
\(
CD < BC
\)
- Hence, the correct answer is that the inequality \( CD < BC \) must always hold true.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A, B,C and D are points on a line such that point B biscets line AC and point A bisects line CD. What is the ratio of AB to CD ?
A1/4B1/3C1/2D2/3
Find the potential difference between the points A and B and between the points B ans C of figure in steady state.
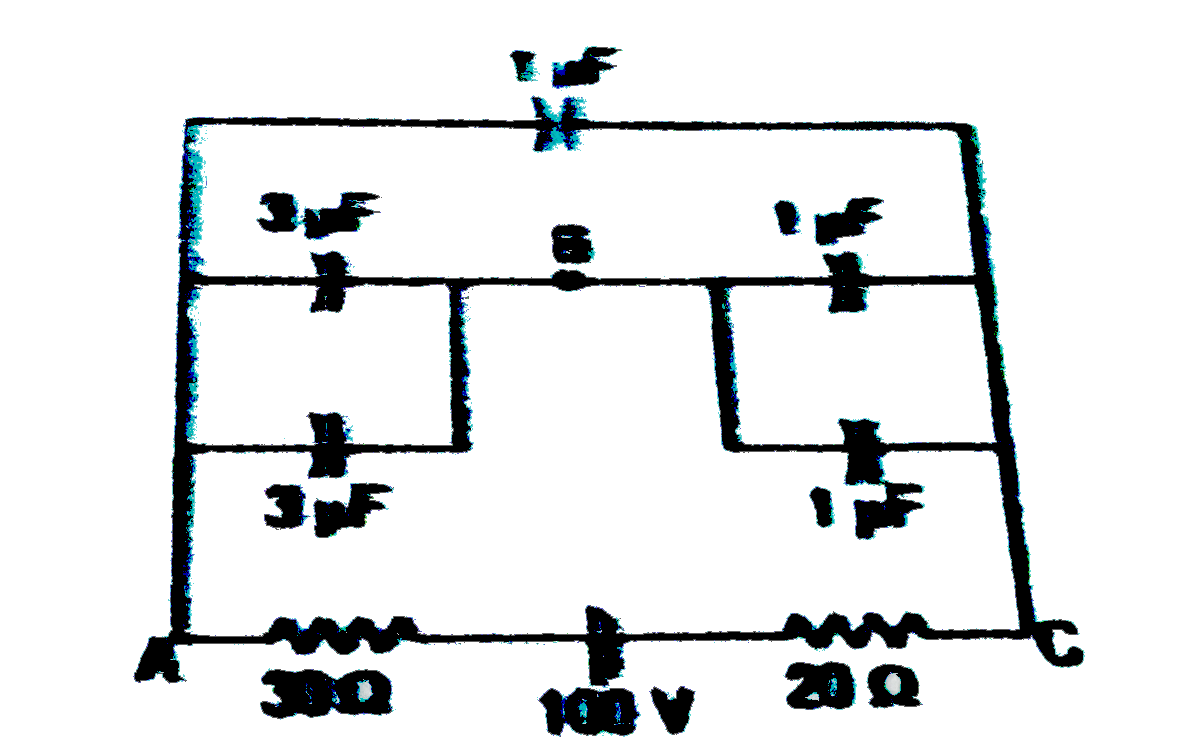
View SolutionCalculate the potential difference between the points A and B, and between the points B and C of figure in steady state
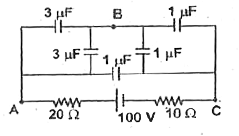
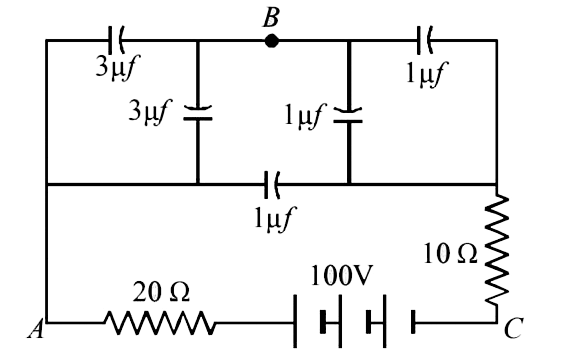
View SolutionIn the diagram shown find the potential difference between the points A and B and between the points B and C in the steady state.
View SolutionTake four distinct point A,B ,C and D , out of which three points are collinear
Name the line segments.
View SolutionPlot the points A(1,-1) and B(4,5).
(i) Draw the line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
View SolutionIf →a,→b,→c&→d are position vector of point A,B,C and D respectively in 3-D space no three of A,B,C,D are colinear and satisfy the relation 3→a−2→b+→c−2→d=0 then (a) A, B, C and D are coplanar (b) The line joining the points B and D divides the line joining the point A and C in the ratio of 2:1 (c) The line joining the points A and C divides the line joining the points B and D in the ratio of 1:1 (d)The four vectors →a,→b,→cand→d are linearly dependent .
View SolutionIf A. B and C are three points on a line, and B lies between A and C then prove that AB+BC=AC.
View Solution

