The temperature, t, in degrees Fahrenheit, in a certain town on a certain spring day satisfies the inequality |t−24|≤30. Which of the followig temperatures , in degrees Fahrenheit, is NOT in this range?
−10
−6
−5
0
The correct Answer is:A
To solve the inequality |t−24|≤30 and determine which temperature is NOT in the specified range, we can follow these steps:
Step 1: Understand the inequality
The inequality |t−24|≤30 means that the distance between t and 24 is at most 30 degrees.
Step 2: Rewrite the absolute value inequality
We can break down the absolute value inequality into two separate inequalities:
−30≤t−24≤30
Step 3: Solve the inequalities
Now we will solve the two inequalities separately.
1. For the left side:
t−24≥−30
Adding 24 to both sides:
t≥−30+24
t≥−6
2. For the right side:
t−24≤30
Adding 24 to both sides:
t≤30+24
t≤54
Step 4: Combine the results
From the two inequalities, we have:
−6≤t≤54
This means that the temperature t must be between -6 degrees Fahrenheit and 54 degrees Fahrenheit, inclusive.
Step 5: Check the options
Now we need to check which of the given temperature options is NOT in the range (−6,54).
Assuming the options provided are:
- A) -10
- B) 0
- C) 30
- D) 55
We can evaluate each option:
- Option A: -10 (Not in the range since -10 < -6)
- Option B: 0 (In the range since -6 ≤ 0 ≤ 54)
- Option C: 30 (In the range since -6 ≤ 30 ≤ 54)
- Option D: 55 (Not in the range since 55 > 54)
Conclusion
The temperature that is NOT in the range is Option A: -10.
---
The inequality |t−24|≤30 means that the distance between t and 24 is at most 30 degrees.
We can break down the absolute value inequality into two separate inequalities:
−30≤t−24≤30
Now we will solve the two inequalities separately.
t−24≥−30
Adding 24 to both sides:
t≥−30+24
t≥−6
t−24≤30
Adding 24 to both sides:
t≤30+24
t≤54
From the two inequalities, we have:
−6≤t≤54
This means that the temperature t must be between -6 degrees Fahrenheit and 54 degrees Fahrenheit, inclusive.
Now we need to check which of the given temperature options is NOT in the range (−6,54).
- A) -10
- B) 0
- C) 30
- D) 55
- Option A: -10 (Not in the range since -10 < -6)
- Option B: 0 (In the range since -6 ≤ 0 ≤ 54)
- Option C: 30 (In the range since -6 ≤ 30 ≤ 54)
- Option D: 55 (Not in the range since 55 > 54)
The temperature that is NOT in the range is Option A: -10.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
C=59(F−32)
The equation above shows how a temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius.
II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
III. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.AI onlyBII onlyCIII onlyDI and II only - Question 2 - Select One
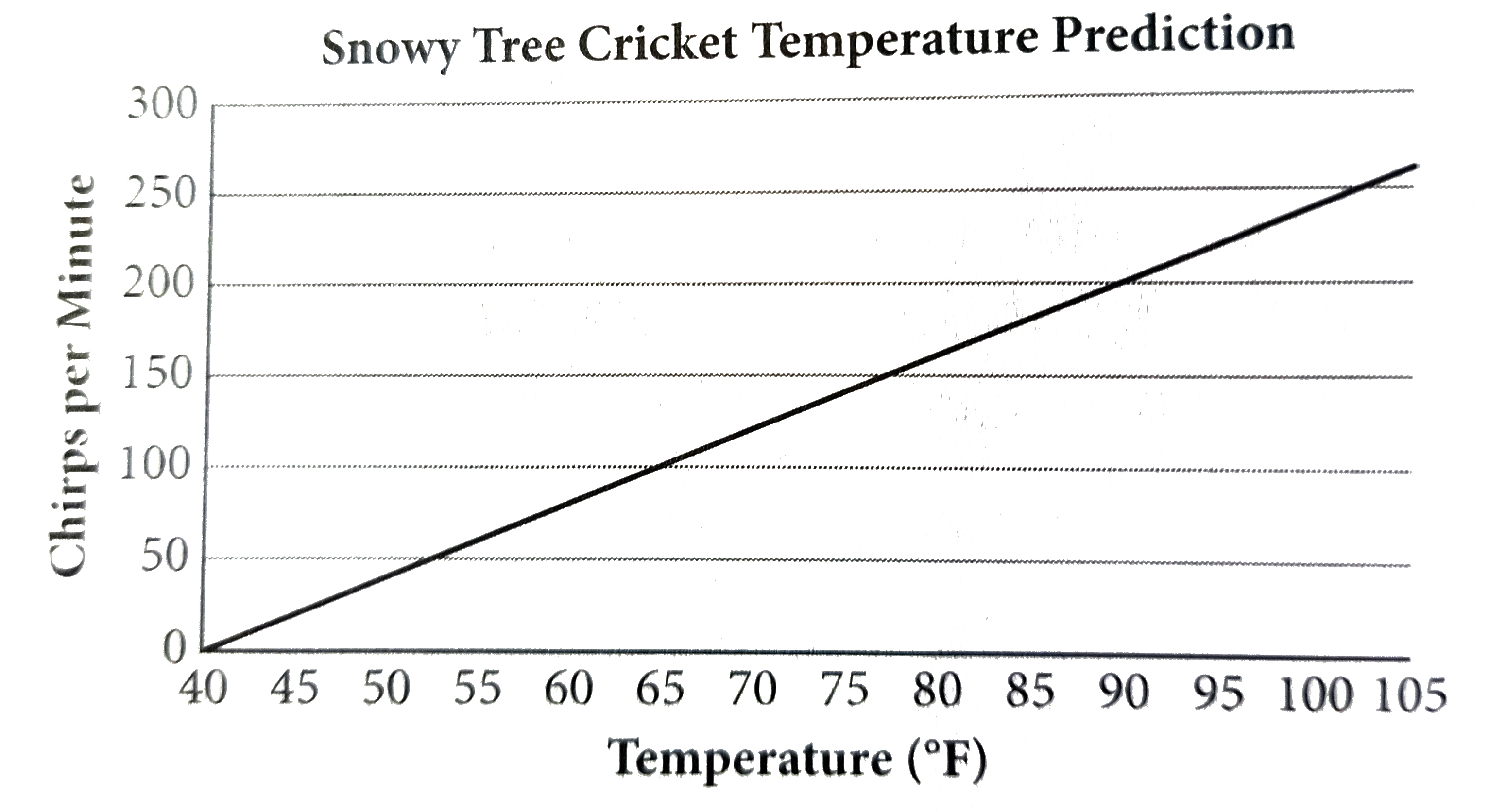
The graph shows the correlation between ambient air temperature, t, in degress Fahrenheit and the number of chirps, c, per minute that a snowy tree cricket makes at that temperature. Which of the following equations represents the line shown in the graph ?Ac=4t−160Bc=14t−160Cc=12t−40Dc=4t+160 - Question 3 - Select One
The relationship between temperature expressed in degrees fahrenheit (F) and degrees Celsius (C) is given by the formula
F=95C+32
If the temperature is 14 degrees Fahrenheit, what is it in degrees Celsius?A−10∘B−12∘C−14∘D−16∘
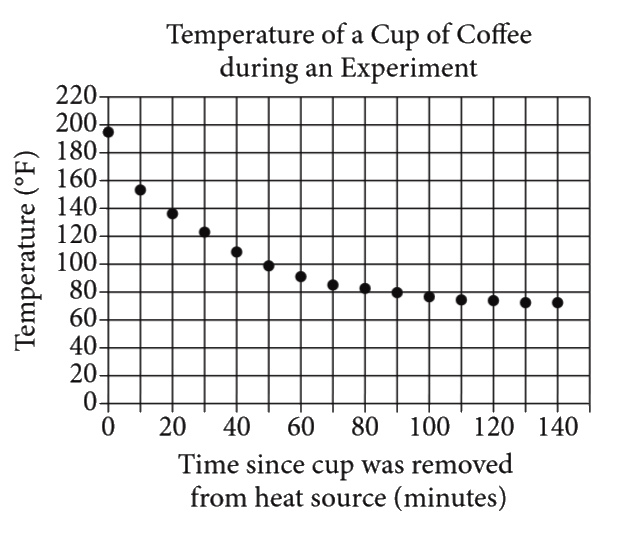
In an experiment, a heated cup of coffee is removed from a heat source, and the cup of coffee is then left in a room that is kept at a constant temperature. The graph above shows the temperature, in degrees Fahrenheit (.∘F), of the coffee immediately after being removed from the heat source and at 10-minute intervals thereafter.
During which of the following 10-minute intervals does the temperature of the coffee decrease at the greatest average rate?View SolutionThe baking time in minutes for a certain cake is defined as VkT, where V is the volume of inches cubed, T is the oven temperature in degrees Fahrenheit, and k is a constant. If the baking time was 30 minutes at 350 degrees Fahrenheit for a cake with a volume of 150 cubic inches, what is the value of constant k?
View Solution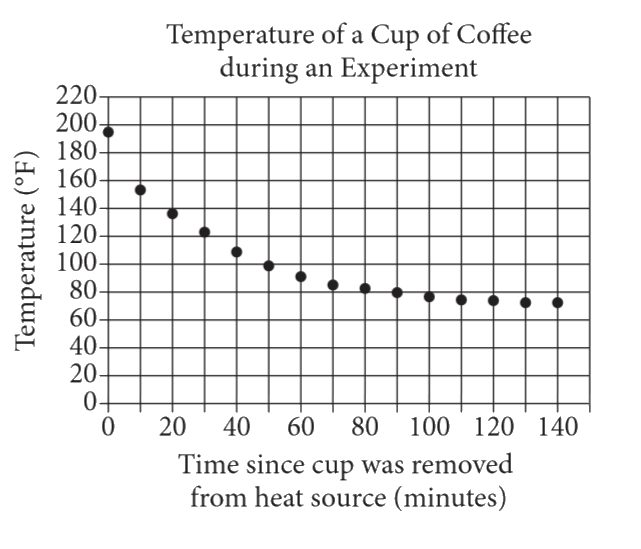
In an experiment, a heated cup of coffee is removed from a heat source, and the cup of coffee is then left in a room that is kept at a constant temperature. The graph above shows the temperature, in degrees Fahrenheit (.∘F), of the coffee immediately after being removed from the heat source and at 10-minute intervals thereafter.
Of the following, which best approximates the temperature, in degrees Fahrenheit, of the coffee when it is first removed from the heat source?View SolutionThe inequality |1.5C−24|≤30 represents the range of monthly average temperature, C, in degrees Celsius, during the winter month for a certain city. What was the lowest monthly average temperature, in degrees Celsius, for for this city?
View SolutionTemperature measured in degrees Fahrenheit (F) are related to temperature measured in degree Celcius (C) by the formula F=95C+32. There is 1 value of x for which x degree Fahrenheit equls x degrees Celsius. What is that value?
View Solution

