Jamie claims, "If a triangle is in Set A, then it is not isosceles." Later, Jamie discovers that △MNP is a counter example proving this claim false. Which of the following statements must be true about △MNP?
It is isosceles and in Set A
It is scalene and in Set A.
It is obtuse and not in Set A.
It is scalene and not in Set A.
The correct Answer is:A
To solve the problem, we need to analyze Jamie's claim and the implications of the counterexample provided by triangle MNP.
1. Understanding Jamie's Claim: Jamie claims, "If a triangle is in Set A, then it is not isosceles." This means that all triangles in Set A are not isosceles triangles.
Hint: Identify the nature of the claim and what it implies about triangles in Set A.
2. Identifying the Counterexample: A counterexample is an example that disproves a claim. Jamie discovers that triangle MNP is a counterexample to the claim. This means that triangle MNP must be isosceles and also part of Set A.
Hint: Recall that a counterexample must directly contradict the original claim.
3. Analyzing Triangle MNP: Since triangle MNP is a counterexample, it must satisfy two conditions:
- It is isosceles (meaning it has at least two equal sides).
- It is in Set A (meaning it belongs to the set that Jamie initially claimed does not contain isosceles triangles).
Hint: Think about the definitions of isosceles triangles and what it means for a triangle to belong to a specific set.
4. Evaluating the Statements: Now, we need to evaluate the statements provided in the options to determine which must be true about triangle MNP. The only statement that aligns with our findings is that triangle MNP is isosceles and in Set A.
Hint: Compare each statement with the conclusions drawn from the counterexample.
5. Concluding the Solution: The only statement that must be true about triangle MNP is that it is isosceles and in Set A. Any other statement that suggests it is scalene or not in Set A contradicts the nature of the counterexample.
Hint: Remember that a valid conclusion must consistently support the disproving of the original claim.
Final Answer:
Triangle MNP is isosceles and in Set A.
- It is isosceles (meaning it has at least two equal sides).
- It is in Set A (meaning it belongs to the set that Jamie initially claimed does not contain isosceles triangles).
Triangle MNP is isosceles and in Set A.
Topper's Solved these Questions
Similar Questions
State which of the following statements are true and which are false :
A triangle has four sides .
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600 If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View Solution
Knowledge Check
In the right triangle shown below, which of the following statements is true about ∠A?
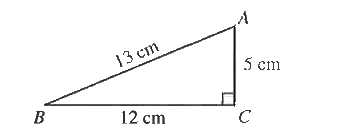 AcosA=1213BsinA=1213CtanA=1213DcosA=1312
AcosA=1213BsinA=1213CtanA=1213DcosA=1312The median of a set of data containing 9 items was found. Four data items were added to the set. Two fo these items were greater that the original median, and the other 2 items were less than the original median. Which of the following statements must be true about the median of the new data set?
AIt is the average of the 2 new lower valuesBIt is the same as the original median .CIt is the average of the 2 new higher values.DIt is greater than the original median.Given the set of data 1,1,2,2,2,3,3,x,y, where x and y represent two different integers. If the mode is 2, which of the following statements must be true?
AIf x=1 or 3, then y must=2BBoth x and y must be gt 3CEither x or Y must =2DIt does not matter what values x and y have
Which of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
View SolutionWhich of the following statements are true (T) and which are false (F): Sum of the three angles of a triangle is 1800 A triangle can have two right angles. All the angles of a triangle can be less than 600 All the angles of a triangle can be greater than 600 All the angles of a triangle can be equal to 600 A triangle can have two obtuse angles. A triangle can have at most one obtuse angles. In one angle of a triangle is obtuse, then it cannot be a right angled triangle. An exterior angle of a triangle is less than either of its interior opposite angles. An exterior angle of a triangle is equal to the sum of the two interior opposite angles. An exterior angle of a triangle is greater than the opposite interior angles
View SolutionWrite of the following statements as true or false? The set of all equilateral triangles is a subset of the set of all isosceles triangles.
View SolutionThe mean of a finite set S of numbers is 14, the median of this set of numbers is 12, and the standard deviation is 1.8. A new set T is formed by multiplying each member of the set S by 3. Which of the following statements must be true of the set T ?
I. The mean of the numbers in set T is 42.
II. The median of the numbers in set T is 36.
III. The standard deviation of the numbers in set T is 5.4.
View SolutionTwo triangles are graphed on a coordinate plane. Triangle MNP has vertices M(−4,2),N(−4,6),andP(−6,2). Triangle QRShasverticesQ(-5, -1), R=(-5, -5), and S(4, -5). Which of the following statements is true?
View Solution
