A parallelogram has a perimeter of 96 inches, and 1 of its sides measures 16 inches. If it can be determined. What are the lengths, in inches, of the other 3 sides?
16, 16, 48
16,24, 24
16,32,32
16,40,40
The correct Answer is:C
To solve the problem, we need to determine the lengths of the sides of the parallelogram given its perimeter and one side length.
1. Understanding the Properties of a Parallelogram:
A parallelogram has opposite sides that are equal in length. If we denote one side as x and the other side as y, then the lengths of the sides can be represented as x,x,y,y.
2. Setting Up the Perimeter Equation:
The perimeter P of a parallelogram is given by the formula:
P=2x+2y
We know from the problem that the perimeter is 96 inches, so we can write:
2x+2y=96
3. Substituting the Known Side Length:
We are given that one of the sides measures 16 inches. Let's assign x=16. Now we can substitute x into the perimeter equation:
2(16)+2y=96
4. Calculating the Value of y:
Simplifying the equation:
32+2y=96
Next, we isolate 2y by subtracting 32 from both sides:
2y=96−32
2y=64
Now, divide both sides by 2 to find y:
y=642=32
5. Listing the Lengths of All Sides:
Now that we have both side lengths, we can summarize:
- One side x=16 inches
- The other side y=32 inches
Therefore, the lengths of the sides of the parallelogram are:
- 16 inches (one side)
- 32 inches (the other side)
- 32 inches (the opposite side)
- 16 inches (the opposite side)
Final Answer:
The lengths of the other three sides of the parallelogram are 16 inches, 32 inches, and 32 inches.
A parallelogram has opposite sides that are equal in length. If we denote one side as x and the other side as y, then the lengths of the sides can be represented as x,x,y,y.
The perimeter P of a parallelogram is given by the formula:
P=2x+2y
We know from the problem that the perimeter is 96 inches, so we can write:
2x+2y=96
We are given that one of the sides measures 16 inches. Let's assign x=16. Now we can substitute x into the perimeter equation:
2(16)+2y=96
Simplifying the equation:
32+2y=96
Next, we isolate 2y by subtracting 32 from both sides:
2y=96−32
2y=64
Now, divide both sides by 2 to find y:
y=642=32
Now that we have both side lengths, we can summarize:
- One side x=16 inches
- The other side y=32 inches
Therefore, the lengths of the sides of the parallelogram are:
- 16 inches (one side)
- 32 inches (the other side)
- 32 inches (the opposite side)
- 16 inches (the opposite side)
The lengths of the other three sides of the parallelogram are 16 inches, 32 inches, and 32 inches.
Topper's Solved these Questions
Similar Questions
A string is cut into 2 pieces that have lengths in the ratio of 2:9. If the difference between the lengths of the 2 pieces of string is 42 inches, what is the lengths in inches of the shorter pieces?
View SolutionA piece of metal is 3 inch (represented by in) long. What is its length in cm?
View Solution
Knowledge Check
A parallelogram has a perimeter of 84 inches, and 1 of its sides measures 16 inches. If it can be determined, what are the lengths, in inches, of the other 3 sides.
A16,16,36B16,18,18C16,26,26D16,34,34A trapezoid has parallel bases that measure 3 inches and 9 inches and a height that measures 6 inches . What is the area, in square inches , of the trapezoid ?
A18B24C30D36For △ABC shown below, base ¯¯¯¯¯¯AC has a length of 16 inches and altitude ¯¯¯¯¯¯BD has a length of 8 inches. The area of a certain square is equal to the area of △ABC. What is the length, in inches, of a side of the square?
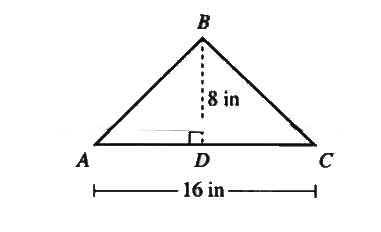 A6B8C12D16
A6B8C12D16
The dimensions of a block of cheese are 12 inches by 3 inches by 3 inches. What is the volume , in cubic inches , of the block of cheese ?
View SolutionThe height of sand in a cylinder-shaped can drops 3 inches foot of sand is poured out. What is the diameter, in inches of the cylinder?
View SolutionWhen each side of a given square is lengthened by 3 inches, the area is increased by 45 square inches. What is the length, in inches, of a sides of the original square?
View SolutionA right triangle has sides measuring 12 inches , 35 inches , and 37 inches . What is the cosine of the angle that lies opposite the 35-inch side ?
View SolutionA right circular cone has a volume of 24π cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
View Solution
