Find the net displacement of a particle from its starting point if it undergoes two sucessive displacement given by →S1=20m,37∘ North of West , →S2=50m,53∘ North of East.
Video Solution
Text Solution
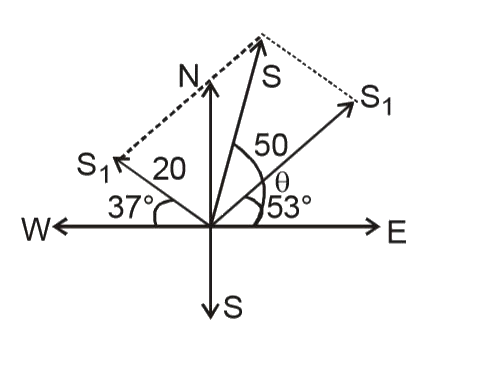
→S=→S1+→S2
Sx=S1x+S2x
=−20cos37∘+50cos53∘=14
Sy=S1y+S2y
=−20sin37∘+50sin53∘=52
S=√S2x+S2y=√(14)2+(52)2=53.85
Angle from west - east axis (x - axis)
tanθ=SySx=5214=267
θ=tan−1(267).
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - PHYSICAL EXAMPLE11videos
VECTOR & CALCULUS
- BOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -176videos
VECTOR & CALCULUS
- BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 318videos
VECTOR
- BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)7videos
WAVE MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle undergoes three successive displacements given by s1=√2 m morth - east , s1=2 m due south and s3=4m,30∘ north of west , then mngnitude of net displecement is
A√14+4√3B√14−4√3C√4DNone of these - Question 2 - Select One
If a man goes 10 m towards north and 20 m towards east then his displacement is
A22.5 m,B25 mC25.5 mD30m - Question 3 - Select One
A man goes 10 m towards North, then 20 m towards east then displacement is
A22.5 mB25mC25.5mD30m
Find the resultant of the following two vector →A and →B.
→A:40 units due east and , →B:25 units 37∘ north of westView SolutionA particle moves 3m north, then 4m east, and then 12m vertically upwards, its displacement is
View SolutionA particle has displacement of 12 m towards east and 5 m towards north then 6 m vertically upwards. The sum of these displacements is
View SolutionA particle has displacement of 12m towards east and 5m towards north then 6m vertically upward. The sum of these displacements is-
View SolutionA man moves 20 m north, then 10m east and then 10√2 m south-west. His displacement is
View Solution

