Find magnitude of →B and direction of →A . If →B makes angle 37∘ and →C makes 53∘ with x axis and →A has magnitude equal to 10 and →c has 5. (given →A+→B+→C=0)
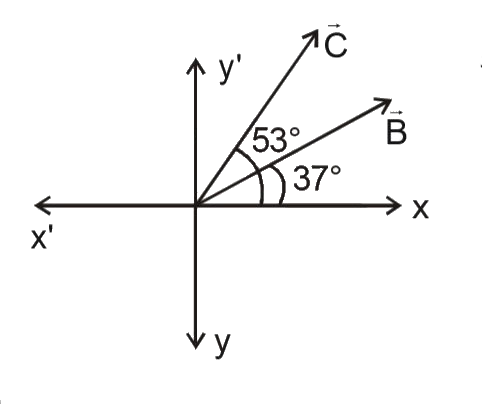
−→A=→C+→B
→A=Axˆi+Ayˆj
⇒−→A=−Axˆi+Ayˆj
⇒Ax=−(Bcos37∘+Ccos53∘)
Ay=−(Bsin37∘+Ccos53∘)
∣∣→A∣∣2=A2x+A2y
A2=(B×45+C×35)2+(B×35+C×45)2
102+(4B5+3)2+(3B5+4)2
⇒100=1625B2+925B2+25+2(3×45+4×35)B
⇒B2+485B−75=0
B = 5 (magnitude can not be negative)
& Angle made by A
⇒Ax=−(205+3)=−12
Ay=−(155+4)=−7
tanθ=AyAx=−7−12
θ=180∘+25∘=205∘.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - PHYSICAL EXAMPLE11videos
VECTOR & CALCULUS
- BOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -176videos
VECTOR & CALCULUS
- BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 318videos
VECTOR
- BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)7videos
WAVE MOTION
Similar Questions
Find →A+→B and →A−→B if →A make angle 37∘ with positive x-axis and →B make angle 53∘ with negative x-axis as shown and magnitude of →A is 5 and of B is 10.
View SolutionThe magnitudes of vectors →A.→B and →C are respectively 12,5 and 13 unira and →A+→B=→C, then the angle between →A and →B is :
View Solution
Knowledge Check
- Question 1 - Select One
The magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and →B is
Aπ2Bcos−1(0.6)Ctan−1(75)Dπ4 - Question 2 - Select One
→A,→Band→C are vectors such that →C=→A+→Band→C⊥→A and also C= A . Angle between →Aand→B is :
Aπ/2Bπ/4C3π/4Dπ - Question 3 - Select One
If →a,→b,→c are vectors such that →a.→b=0 and →a+→b=→c then:
A|→a|2+∣∣→b∣∣2=|→c|2B|→a|2=∣∣→b∣∣2+|→c|2C∣∣→b∣∣2=|→a|2+|→c|2DNone of these
A magnitude of vector →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is
View SolutionIf →A=→B+→C and the magnitudes of →A,→Band→C are 5,4 and 3 units respecetively, the angle between →A and →C is :
View SolutionIf →A+→B=→C, then magnitude of →B is
View SolutionIf →a+2→b+3→c=→0 then →a×→b+→b×→c+→c×→a=
View Solution→A,→Band→C are vectosrs each having a unit magneitude. If →A+→B+→C=0, then →A.→B.→C+→C.→A will be:
View Solution

