Consider eight small spheres , radius = arranged at the corner of the cube , they are small enough so that they are not in contact . Now place a larger sphere , radius = at the centre of the cube . This sphere is just large enough so that it is in contact with the eight small sphere . Now let the radius of the large sphere shrink , but keep the small sphere in contact with it . what is the radius ratio , when the small spheres at the cube corners come in to contact with each other .

The correct Answer is:C
Similar Questions
Knowledge Check
A large insulated sphere of radius r charged with Q units of electricity is placed in contact with a small insulated uncharged sphere of radius r' and is then separated. The charge on the smaller sphere will now be.
AQ(r'+r)r'BQ(r'+r)rCQrr'+rDQr'r'+rThe ratio of total surface area and volume of a sphere is 1 : 7. This sphere is melted to form small spheres of equal size. The radius of each small sphere is 1/6th the radius of the large sphere. What is the sum (in cm2) of curved surface areas of all small spheres?
A31276B36194C25182D33264A solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres . The ratio of the surface area of this sphere to that of a small sphere is
A4:1B1:16C16:1D1:4
Find the volume of the larges cylinder that can be inscribed in a sphere of radius r
View SolutionA large insulated sphere of radius r charged with Q units of electricity is placed in contact with a small insulated uncharged sphere of radius r' and is then separated. The charge on the smaller sphere will now be.
View SolutionA small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
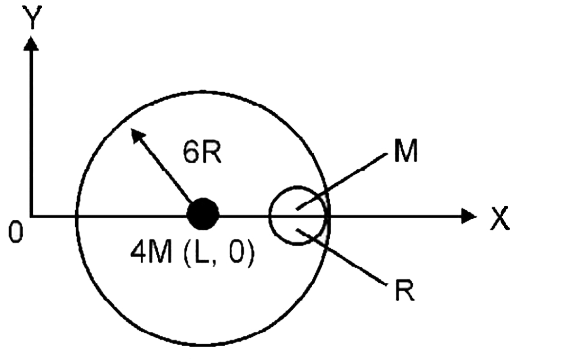
View SolutionEight point charge of charge q each are placed on the eight corners of a cube of side a. A solid neutral metallic sphere of radius a/3 is placed with its centre at the centre of the cube . As a result charges are induced on the sphere , which form certain pattern on its surface . What is the potential at the center of the sphere .
View SolutionThe edge of a cube is equal to the radius of a sphere. If the edge and the radius increase at the same rate, then the ratio of the increases in surface areas of the cube and sphere is
View Solution
