The acceleration of a particle which is depend on time is given by following function a = 2t + 1 and at time t = 0, x = 1m and ui = 2m/s. Then find out displacement of the particle at t = 3 sec.
To solve the problem, we need to find the displacement of a particle given its acceleration as a function of time, initial position, and initial velocity. Here’s a step-by-step solution:
Step 1: Understand the given information
- Acceleration a(t)=2t+1
- Initial position x(0)=1m
- Initial velocity u=2m/s
- Time t=3s
Step 2: Find the velocity as a function of time
To find the velocity, we need to integrate the acceleration function with respect to time.
a=dvdt⟹dv=adt=(2t+1)dt
Integrating both sides:
∫dv=∫(2t+1)dt
This gives:
v=t2+t+C
Where C is the constant of integration. To find C, we use the initial condition v(0)=2m/s:
v(0)=02+0+C=2⟹C=2
Thus, the velocity function is:
v(t)=t2+t+2
Step 3: Find the position as a function of time
Next, we integrate the velocity function to find the position:
v=dxdt⟹dx=vdt=(t2+t+2)dt
Integrating both sides:
∫dx=∫(t2+t+2)dt
This gives:
x=t33+t22+2t+D
Where D is another constant of integration. To find D, we use the initial condition x(0)=1:
x(0)=0+0+0+D=1⟹D=1
Thus, the position function is:
x(t)=t33+t22+2t+1
Step 4: Calculate the position at t=3s
Now we substitute t=3 into the position function:
x(3)=333+322+2(3)+1
Calculating each term:
=273+92+6+1
=9+4.5+6+1
=20.5m
Step 5: Find the displacement
Displacement is defined as the change in position:
Displacement=x(3)−x(0)=20.5−1=19.5m
Final Answer
The displacement of the particle at t=3s is 19.5m.
---
- Acceleration a(t)=2t+1
- Initial position x(0)=1m
- Initial velocity u=2m/s
- Time t=3s
To find the velocity, we need to integrate the acceleration function with respect to time.
Next, we integrate the velocity function to find the position:
Now we substitute t=3 into the position function:
=9+4.5+6+1
=20.5m
Displacement is defined as the change in position:
The displacement of the particle at t=3s is 19.5m.
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
Two particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
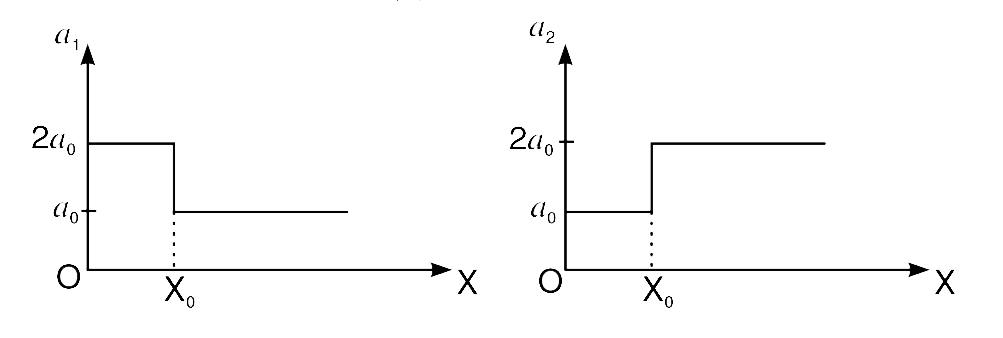
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution
Knowledge Check
The displacement of a particle in time t is given by s=2t2−3t+1. The acceleration is
A1B3C4D5The acceleration a of α of a particle depends on displacements covered in a time t as a=S+5 . It is given that initially S=0 m and v=5m/s. Then
Av=S+5Bv=√S+5Ct=loge(S+5S)Dt=loge(S+55)The acceleration of a particle is given by a = 3t and at t = 0, v = 0, x = 0. The velocity and displacement at t = 2 sec will be-
A6 m/s, 4 mB4 m/s, 6 mC3 m/s, 2 mD2 m/s, 3 m
The acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionIf velocity is depend on time such that v = 4 – 2t. Find out distance travelled by particle from 1 to 3 sec
View SolutionA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to t=t1 will be
View SolutionThe displacement s of a particle at time t is given by s=αsinωt+βcosωt then acceleration at time t is
View SolutionThe velocity of the particle at any time t is given by vu=2t(3−t)ms−1. At what time is its velocity maximum?
View Solution
