A particle is projected at an angle ∝ with horizontal from the foot of a plane whose inclination to β Show that it will strike the plane at right angles if cotβ=2tan(∝−β)
Let u be the velocity of projection so that u cos (∝−β) and u sin (∝−β) are the initial velocities respectively parallel and perpendicular to the inclined plane. The acceleration in these two directions are (–gsinβ) and (–gcosβ). The initial component of velocity perpendicular to PQ is u sin (∝−β) and the acceleration in this direction is (–gcosβ). If T is the time the particle takes to go from P to Q then in time T the space described in a direction perpendicular to PQ is zero.
0=usin(∝−β).T−12gcosβT2
T=2usin(∝−β)gcosβ
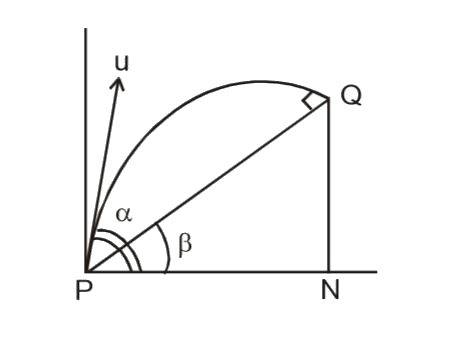
If the direction of motion at the instant when the particle hits the plane be perpendicular to the plane, then the velocity at that instant parallel to the plane must be zero.
∴ucos(∝−β)−gsinβT=0
(ucos(∝−β)gsinβ=T=(2usin(∝−β)gcosβ
∴cosβ=2tan(∝−β)
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizon. Show that
(a) tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(b) tan∝=2tanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
View Solution
Knowledge Check
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
Atan(α−β)=cotβB2tan(α−β)=cotβC2cot(α−β)=cotβDNone of theseA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3)A particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3)
A projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
View SolutionA shot is fired at an angle α to the horizontal up a hill of inclination β to the horizontal. Then it strikes the hill horizontally if
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle is projected from a point A with velocity u√2 at an angle of 45∘ with horizontal as shown in the figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View Solution