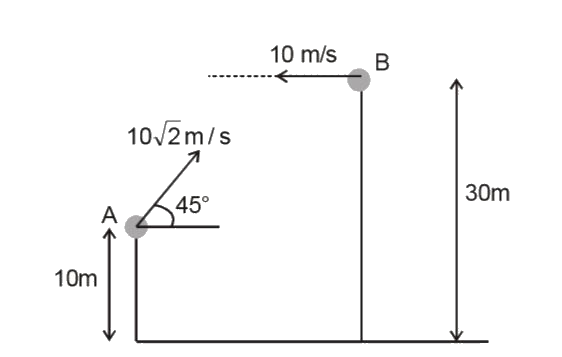
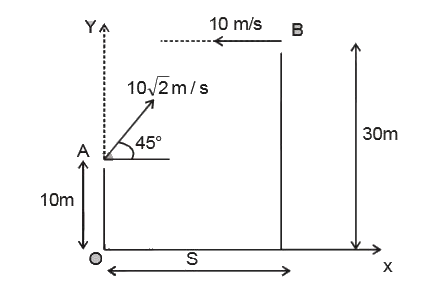
Two projectiles are projected simultaneously from two towers as shwon in figure. If the projectiles collide in the air, then find the distance "s" between the towers.
Video Solution
Text Solution
We see here that projectiles are approaching both horizontally and vertically. Their movement in two component directions should be synchronized so that they are at the same position at a particular given time. For collision, the necessary requirement is that relative velocity and displacement should be in the same direction. It is given that collision does occur. It means that two projectiles should cover the displacement with relative velocity in each of the component directions. In x-direction,
vAB=uAx−uBx=10√2cos45∘−(−10)
=10√21√2+10=20m/s
if "t" is time after which collision occurs, then
⇒s=vAy−uBy
⇒vABy=ucos45∘−0=10√2×1√2=10m/s
The initial vertical distance between points of projection is 30 – 10 = 20 m. This vertical distance is covered with component of relative velocity in vertical direction. Hence, time taken to collide, "t", is :
⇒t=2010=2
Putting this value in the earlier equation for "s", we have :
⇒s=20t=20×2=40m
|
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
Knowledge Check
Two particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
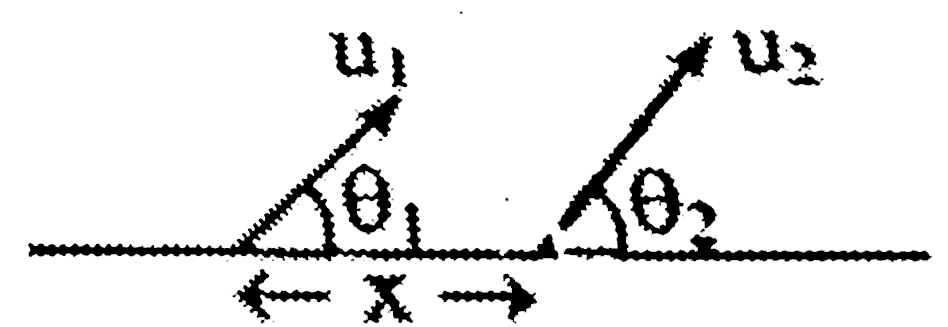 Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)Two particles are projected simultaneously from the top of the towers as shown. Find the distance between the towers if they collide in mid air during their flight.
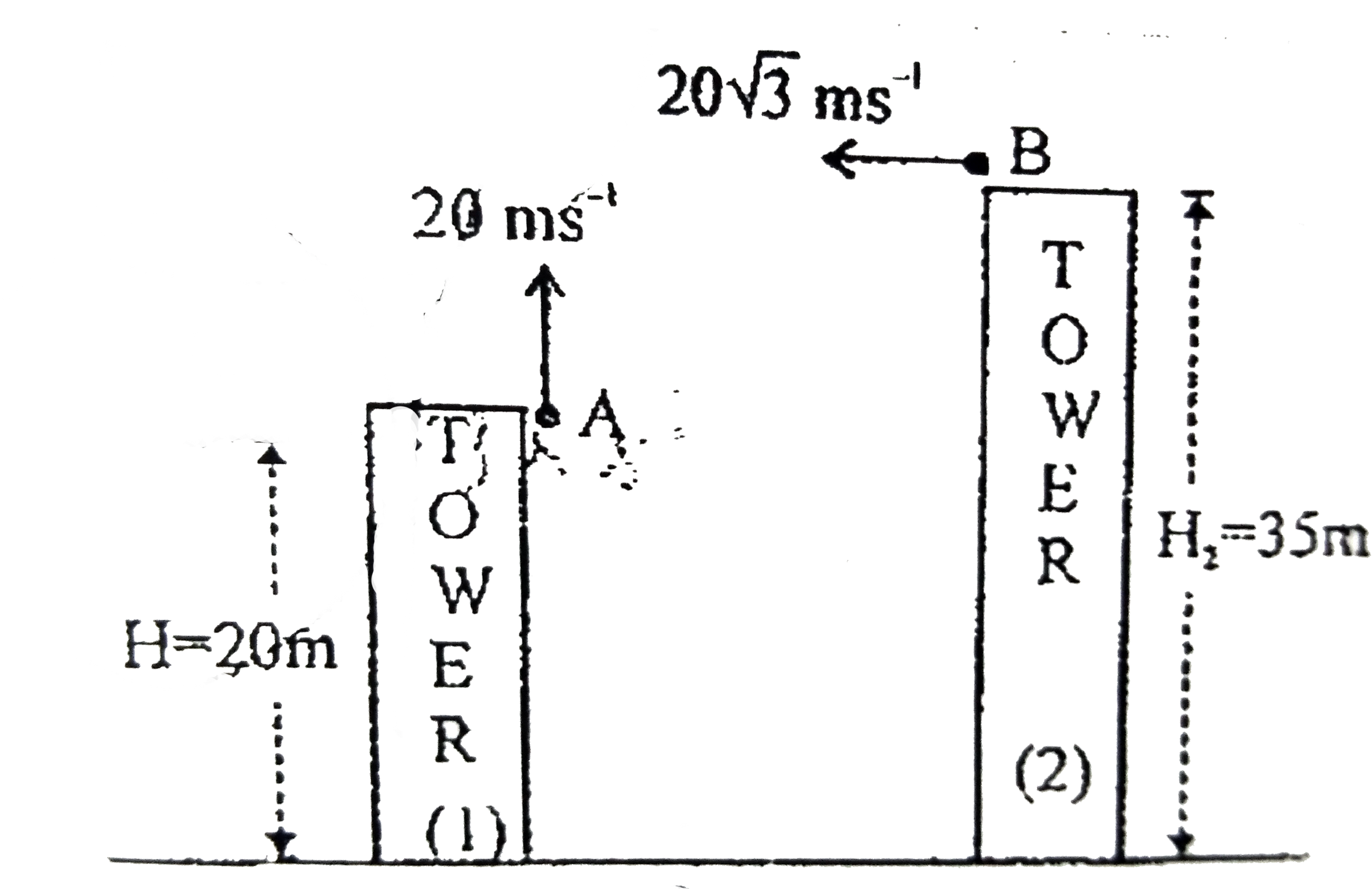 A15mB20mC15√3mD5√3m
A15mB20mC15√3mD5√3mTwo projectiles A and B are fired simultaneously as shown in figure. They collide in air at point at time t.Then
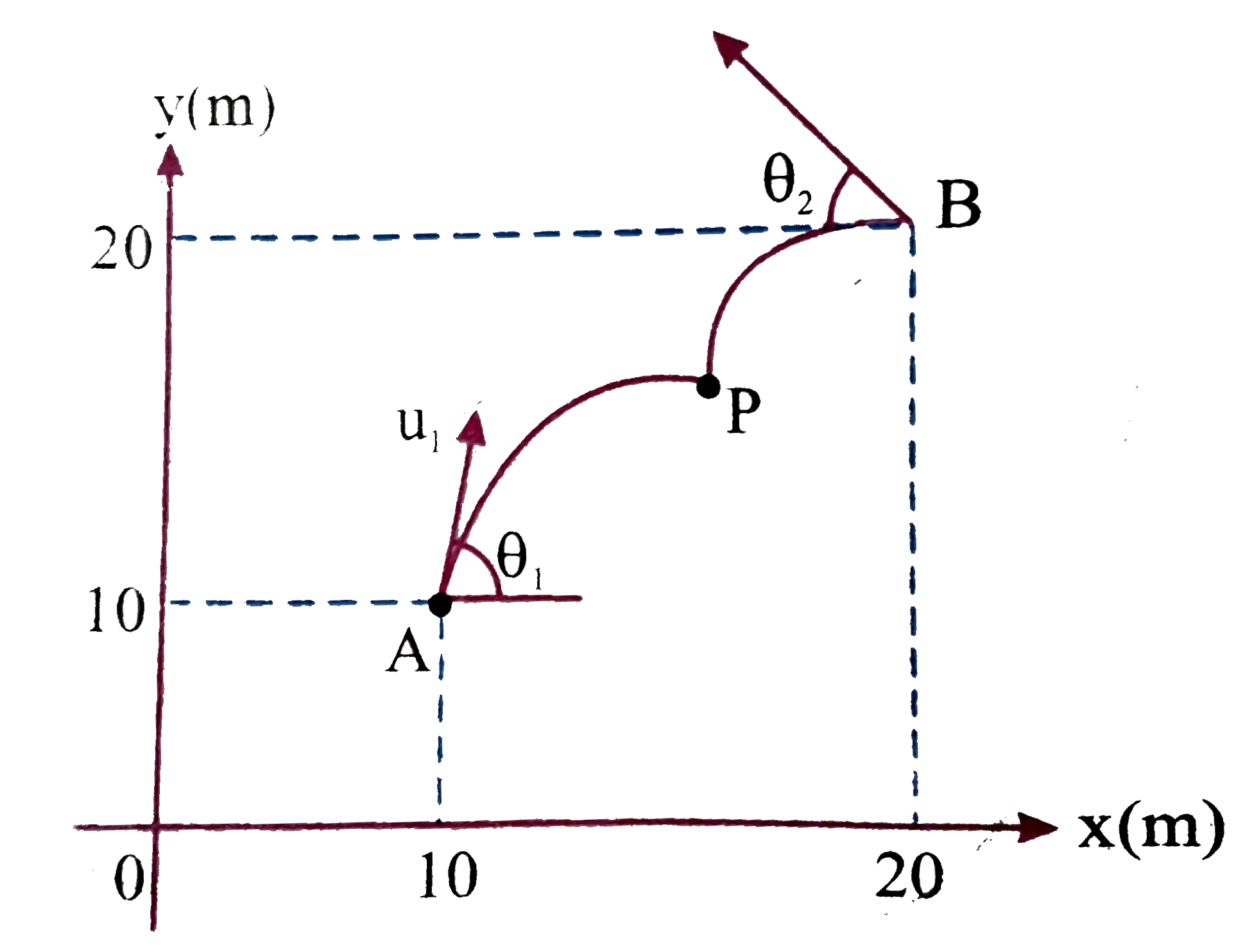 At(u1cosθ1−u2cosθ2)=20Bt(u1sinθ1−u2sinθ2)=10CBoth (a) and (b) are correctDBoth (a) and (b) are wrong
At(u1cosθ1−u2cosθ2)=20Bt(u1sinθ1−u2sinθ2)=10CBoth (a) and (b) are correctDBoth (a) and (b) are wrong
Projectile from Height, Projectile from Tower
View SolutionTwo particles are projected from the two towers simultaneously, as shown in the figure. What should be value of 'd' for their collision.

View SolutionTwo particles are projected from the two towers simultaneously, as shown in the figure.

What should be value of 'd' for their collision.
View SolutionTwo stones are projected simultaneously from a tower a differenct angles of projection with same speed 'u'. The distance between two stones is increasing at constant rate 'u'. Then the angle between the initial velocity vectors of the two stones is :
View SolutionThere are two towers of 5m&10m. The line joining there tops makes 15∘ with ground then find the distance between them
View Solution
