Three stones A, B and C are simultaneously projected from same point with same speed. A is thrown upwards, B is thrown horizontally and C is thrown downwards from a building. When the distance between stone A and C becomes 10 m, then distance between A and B will be :
10m
5m
10sqrt(2) m
5sqrt(2) m
The correct Answer is:D
To solve the problem, we need to analyze the motion of the three stones A, B, and C, which are thrown from the same point with the same initial speed but in different directions.
1. Identify the motion of each stone:
- Stone A is thrown upwards.
- Stone B is thrown horizontally.
- Stone C is thrown downwards.
2. Define the time of flight:
Let the time of flight for all stones be t.
3. Calculate the vertical displacement of each stone:
- For stone A (upwards):
SA=ut−12gt2
- For stone B (horizontal):
- Vertical displacement (due to gravity):
SBv=12gt2
- Horizontal displacement:
SBh=ut
- For stone C (downwards):
SC=ut+12gt2
4. Determine the distance between stones A and C:
Given that the distance between stones A and C is 10 m:
|SA−SC|=10
Substituting the equations for SA and SC:
|(ut−12gt2)−(ut+12gt2)|=10
Simplifying this gives:
|−gt2|=10
Thus:
gt2=10(since distance cannot be negative)
5. Calculate the value of ut:
From the previous step, we have:
ut=10g(using g=10m/s2 for simplicity)
Therefore:
ut=5m
6. Find the distance between stones A and B:
The vertical distance of stone B from the original point is:
SBv=12gt2=12×10×t2=5m
The horizontal distance of stone B is:
SBh=ut=5m
7. Calculate the resultant distance between A and B:
Using the Pythagorean theorem:
dAB=√(SBh)2+(SBv)2=√(5)2+(5)2=√25+25=√50=5√2m
Final Answer:
The distance between stone A and stone B when the distance between stone A and stone C becomes 10 m is 5√2m.
- Stone A is thrown upwards.
- Stone B is thrown horizontally.
- Stone C is thrown downwards.
Let the time of flight for all stones be t.
- For stone A (upwards):
SA=ut−12gt2
- For stone B (horizontal):
- Vertical displacement (due to gravity):
SBv=12gt2
- Horizontal displacement:
SBh=ut
- For stone C (downwards):
SC=ut+12gt2
Given that the distance between stones A and C is 10 m:
|SA−SC|=10
Substituting the equations for SA and SC:
|(ut−12gt2)−(ut+12gt2)|=10
Simplifying this gives:
|−gt2|=10
Thus:
gt2=10(since distance cannot be negative)
From the previous step, we have:
ut=10g(using g=10m/s2 for simplicity)
Therefore:
ut=5m
The vertical distance of stone B from the original point is:
SBv=12gt2=12×10×t2=5m
The horizontal distance of stone B is:
SBh=ut=5m
Using the Pythagorean theorem:
dAB=√(SBh)2+(SBv)2=√(5)2+(5)2=√25+25=√50=5√2m
The distance between stone A and stone B when the distance between stone A and stone C becomes 10 m is 5√2m.
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS (Level-2)
26 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
6 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
Three identical balls are thrown from the top of a building, all with the same initial speed. As shown in figure., the first ball is thrown horizontally, second above horizontal level, and third at an angle below the horizontal. Neglecting air resistance, rank the speeds of the balls at the instant each hits the ground.

View SolutionThree stones are projected simultaneously with same speed u from the top of a tower. Stone 1 is projected horizontally and stone 2 and stone 3 are projected making an angle q with the horizontal as shown in fig. Before stone 3 hits the ground, the distance between 1 and 2 was found to increase at a constant rate u.
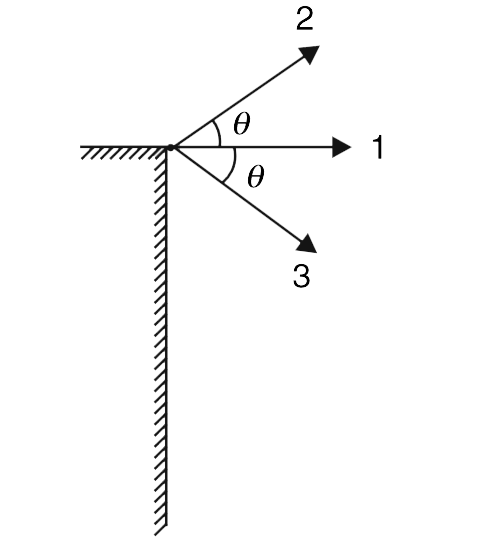
(a) Find θ
(b) Find the rate at which the distance between 2 and 3 increases.
View Solution
Knowledge Check
Thre stones A, B and C are simultaneously projected from same point with same speed. A is thrown upwards, B is thrown horizontally and C is thrown downwards from a boulding. When the distance between stone A and C becomes 10 m, then distance between A and B will be-
A10 mB5 mC5√2mD10√2mAssertion:- Two stones are simultaneously projected from level ground from same point with same speeds but different angles with horizontal Both stones move in same vertical plane. Then the two stones may collide in mid air.
Reason:- For two stones projected simultaneously from same point with same speed at different angles with horizontal, their trajectories must intersect at some point except projection point.AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are False.Two balls AandB of same masses are thrown from the top of the building A. Thrown upward with velocity VandB, thrown downward with velocity V, then
AVelocity of A is more than B at the groundBVelocity of B is more than A at the groundCBoth AandB strike the ground with same velocityDNone of these
From the top of a tower, a stone A is thrown upwards and a stone B is thrown downwards with the same speed. The velocity of stone A, on colliding with the ground is :
View SolutionTwo bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
View SolutionTwo projectiles A and B are thrown from the same point with velocities v and v2 respectively. If B is thrown at an angle 45∘ with horizontal.What is the inclination of A.when their ranges are the same?
View Solution
A stone is projected from point A with speed u making an angle 60∘ with horizontal as shown. The fixed inclined suface makes an angle 30∘ with horizontal. The stone lands at B after time t. Then the distance AB is equal to
View SolutionTwo stones are projected simultaneously from a tower a differenct angles of projection with same speed 'u'. The distance between two stones is increasing at constant rate 'u'. Then the angle between the initial velocity vectors of the two stones is :
View Solution
