The area bounded by the curve $y = \frac{3}{| x |} and y + | 2 - x | = 2$ is

Video Solution

Text Solution

Verified by Experts

$y^{2} (2 - x) = x^{2}$
$∴ y^{2} = \frac{x^{3}}{2 - x}$
$∴ y = \pm \frac{x^{3 / 2}}{\sqrt{2 - x}}, clearly x \in [0, 2]$
$Consider y = \frac{x^{3 / 2}}{\sqrt{2 - x}}$
When x=0, y=0
Also, when x increases from $' 0' to' 2', y increases from '0' \to' \infty'$
Hence graph of given relation is as shown in the following figure :

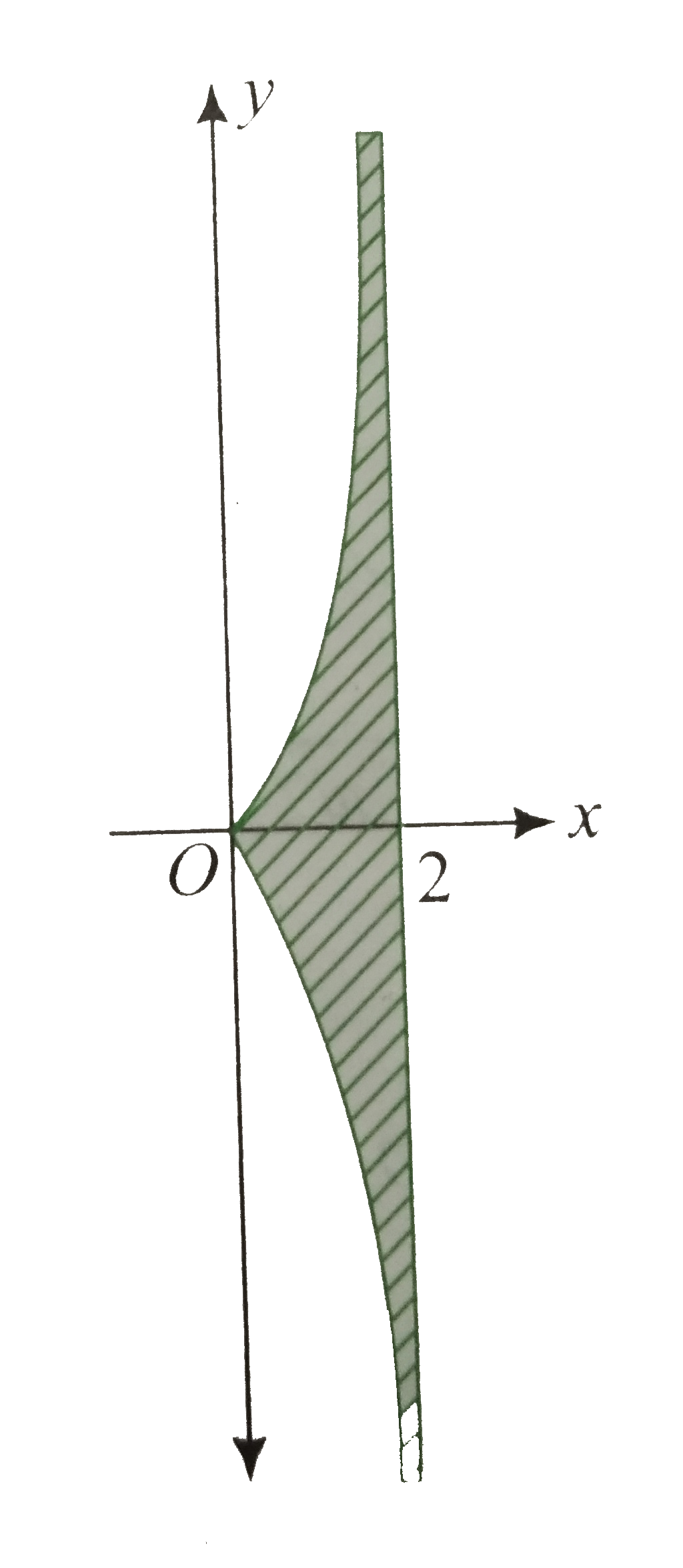
$Required Area is A = 2 2 \int 0 \frac{x^{3 / 2}}{\sqrt{2 - x}} d x$
$Put x = 2 {sin}^{2} θ$
$∴ A = 2 π / 2 \int 0 \frac{2 \sqrt{2} {sin}^{3} θ}{\sqrt{2 - 2 {sin}^{2} θ}} 4 sin θ cos θ d θ$
$= 16 π / 2 \int 0 {sin}^{4} θ d θ$
$= 16 π / 2 \int 0 \frac{{(1 - cos 2 θ)}^{2}}{4} d θ$
$= 4 π / 2 \int 0 (1 - 2 cos 2 θ + {cos}^{2} 2 θ) d θ$
$= 4 π / 2 \int 0 (1 - 2 cos 2 θ + \frac{1 + cos 4 θ}{2}) d θ$
$= 4 {⎛ ⎝ θ + sin 2 θ + \frac{θ + \frac{sin 4 θ}{4}}{2} ⎞ ⎠}_{0}^{π / 2}$
$= 4 (\frac{π}{2} + 0 + \frac{π}{4})$
$= 3 π$

Updated on:21/07/2023

The area bounded by the curves $y = x^{2} and y = 2 - x^{2}$ is
A $\frac{8}{3}$ sq units
B $3 / 8$ sq units
C $3 \frac{/}{2}$ sq units
DNone of these
The area bounded by the curves $y^{2} = x^{3} and | y | = 2 x$ is
A $\frac{5}{16}$ sq units
B $\frac{16}{5}$ sq units
C $\frac{3}{8}$ sq units
DNone of these