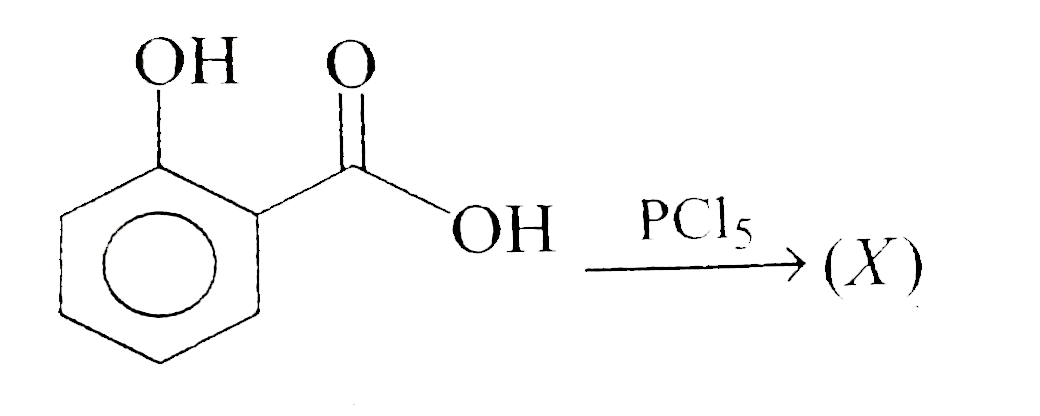
(X) will be :

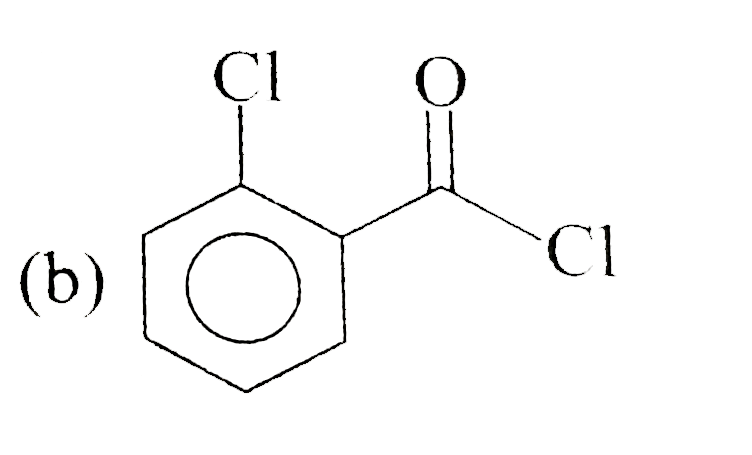
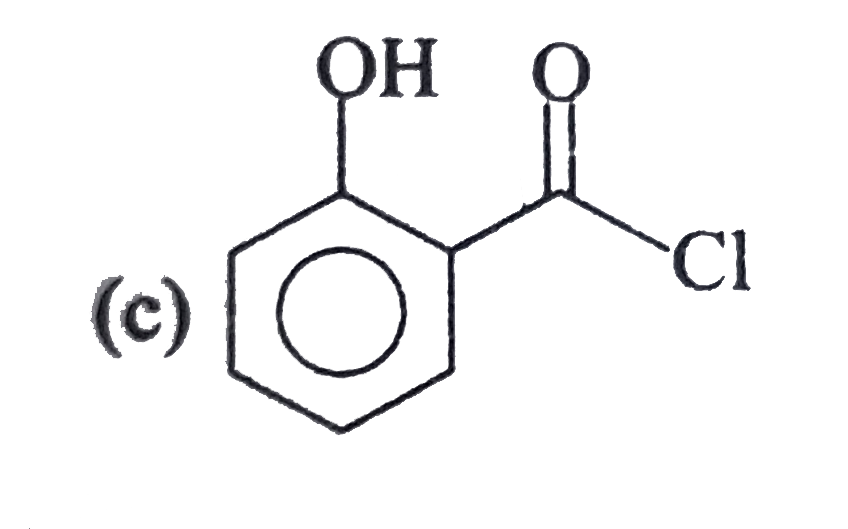
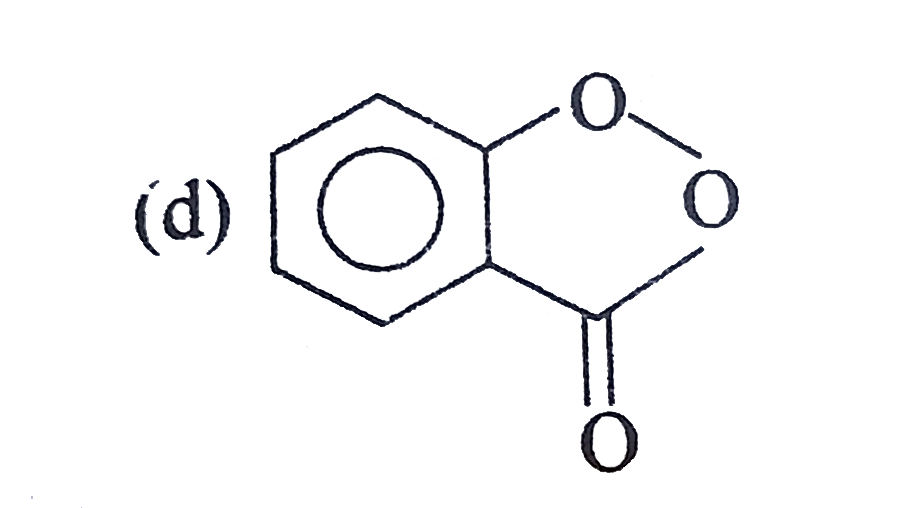
The correct Answer is:C
Step by step video, text & image solution for (X) will be : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - HIMANSHU PANDEYCHAPTER - CABOXYLIC ACIDS AND ITS DERIVATIVESEXERCISE - Level 2 (Q.26 To Q.50)25videos
CABOXYLIC ACIDS AND ITS DERIVATIVES
- BOOK - HIMANSHU PANDEYCHAPTER - CABOXYLIC ACIDS AND ITS DERIVATIVESEXERCISE - Level 2 (Q.51 To Q.75)25videos
CABOXYLIC ACIDS AND ITS DERIVATIVES
- BOOK - HIMANSHU PANDEYCHAPTER - CABOXYLIC ACIDS AND ITS DERIVATIVESEXERCISE - Level 1 (Q.27 To Q.50)24videos
CABOXYLIC ACIDS AND ITS DERIVATIVES
- BOOK - HIMANSHU PANDEYCHAPTER - BIOMOLECULESEXERCISE - Match The Column6videos
BIOMOLECULES
- BOOK - HIMANSHU PANDEYCHAPTER - CARBONYL COMPOUNDSEXERCISE - Subjective Type Problems10videos
CARBONYL COMPOUNDS
Similar Questions
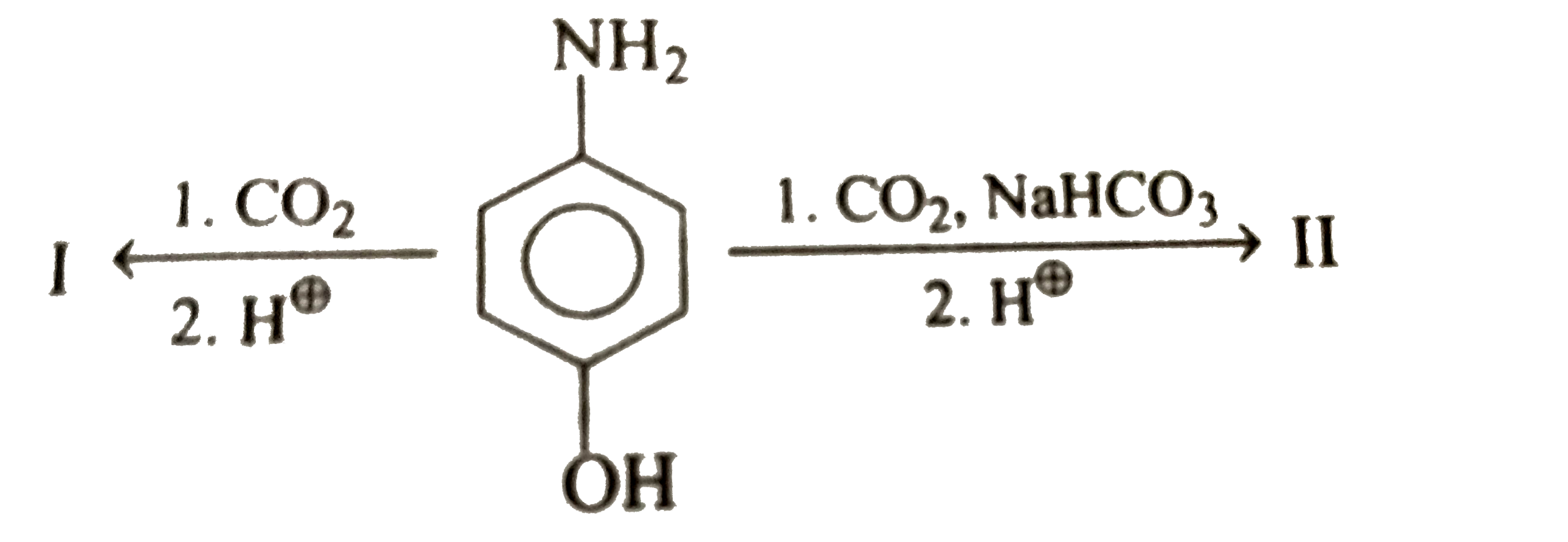
Product I and II are respectively:02:39View SolutionWhat is the major product obtained in this reaction ?
 02:42View Solution
02:42View SolutionX and Y in the reaction sequence R−C≡NH3O⊕−−−→Xdiazomethane−−−−−−−→Y ,are given by the set:
02:38View Solution
 View Solution
View SolutionFind out final product of following reaction :
 03:09View Solution
03:09View SolutionUsing properties of determinants, solve for x|[a+x,a−x,a−x],[a−x,a+x,a−x],[a−x,a−x,a+x]∣=0
02:09View Solutionx^(x sqrt(x))=(x sqrt(x))^(x), then x is equal to
04:22View Solution|[x+3,x,x] , [x,x+3,x] , [x,x,x+3]|=27(x+1)
05:25View SolutionIf ∣∣ ∣ ∣ ∣∣αxxxxβxxxxγxxxxδ∣∣ ∣ ∣ ∣∣=f(x)−xf'(x) then f(x) is equal to
03:08View SolutionIf ∣∣ ∣∣a+xa−xa−xa−xa+xa−xa−xa−xa+x∣∣ ∣∣=0, then x is equal to
04:38View Solutionसरणिको के गुणों का प्रयोग करके निम्न को x के लिए हल कीजिएः। ∣∣ ∣∣x+axxxx+axxxx+a∣∣ ∣∣=0
04:27View Solutionx का मान निकाले ∣∣ ∣∣xxx+axx+axx+axx∣∣ ∣∣=0
04:23View Solutionसिद्ध कीजिए कि -
∣∣ ∣∣x+9xxxx+9xxxx+9∣∣ ∣∣=243(x+3).04:18View SolutionUsing Properties of determinants, solve the following for x:
∣∣ ∣∣x+axxxx+axxxx+a∣∣ ∣∣=003:00View SolutionUsing properties of determinants, solve for x|[a+x,a−x,a−x],[a−x,a+x,a−x],[a−x,a−x,a+x]∣=0
04:07View SolutionUsing properties of determinants, solve for x|[a+x,a−x,a−x],[a−x,a+x,a−x],[a−x,a−x,a+x]∣=0
04:08View Solution

