Find ∫xcosxdx
To find the integral ∫xcosxdx, we will use the method of integration by parts. The integration by parts formula is given by:
∫udv=uv−∫vdu
Step 1: Choose u and dv
We choose:
- u=x (which we will differentiate)
- dv=cosxdx (which we will integrate)
Step 2: Differentiate u and Integrate dv
Now we differentiate u and integrate dv:
- du=dx
- v=∫cosxdx=sinx
Step 3: Apply the Integration by Parts Formula
Now we apply the integration by parts formula:
∫xcosxdx=uv−∫vdu
Substituting the values we have:
∫xcosxdx=xsinx−∫sinxdx
Step 4: Integrate sinx
Now we need to compute ∫sinxdx:
∫sinxdx=−cosx
Step 5: Substitute Back
Substituting this back into our equation gives:
∫xcosxdx=xsinx−(−cosx)
This simplifies to:
∫xcosxdx=xsinx+cosx+C
where C is the constant of integration.
Final Answer
Thus, the final result is:
∫xcosxdx=xsinx+cosx+C
---
- u=x (which we will differentiate)
- dv=cosxdx (which we will integrate)
- du=dx
- v=∫cosxdx=sinx
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.122videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.86videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.324videos
INTEGRALS
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
- BOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE17videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
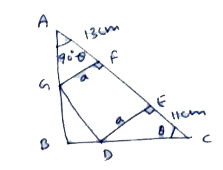
Find x
 A110°B150∘C100°D105°
A110°B150∘C100°D105° - Question 2 - Select One
Find x
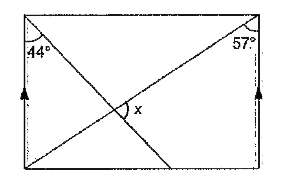 A78∘B80∘C75∘D79∘
A78∘B80∘C75∘D79∘ - Question 3 - Select One
Find x
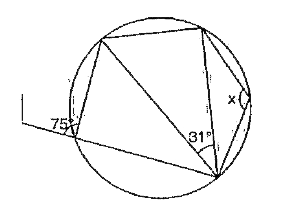 A110∘B104∘C108∘D106∘
A110∘B104∘C108∘D106∘