The point to which the origin should be shifted in order to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0 is Solution in Telugu
only 1 is true
only II is true
both I and II are true
neither I nor II are true
The correct Answer is:B
Step by step video, text & image solution for The point to which the origin should be shifted in order to eliminate x and y terms in the equation 4x^(2) + 9y^(2) - 8x + 36y +4=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSFORMATION OF AXES BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-2
3 Videos
- TRANSFORMATION OF AXES BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-3
2 Videos
- TRANSFORMATION OF AXES BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - EXCERSIE 1
64 Videos
- THEORY OF EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 4
4 Videos
- TRIGONOMETRIC EQUATIONS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
4 Videos
Similar Questions
If the transformed equation of 6x2+5xy−6y2=0 when the axes are translated to the pont (-1,-1) is 6X2+5XY−6Y2+aX+bY+c=0 then the descending order of a,b,c is
View SolutionTo remove the first degree terms in the following equation origin should be shifted to the another point then calculate the new origins is
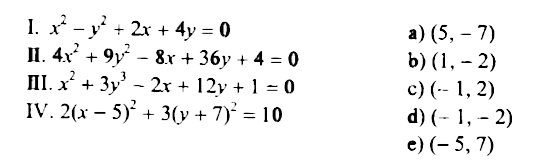
View SolutionThe coordinates of the point (3,-5) in the new system when the origin is shifted to (−2,3) are
View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.
View SolutionA : The general solution of sinx=−1 is nπ+(−1)n3π2,n∈Z
R : The principal solution of sin x = 0 lies in [−π/2,π/2]
View SolutionTo remvoe the first dgree terms in the equation 4x2+9y2−8x+36y+4=0, the origin in shifted to the point
View SolutionThe point to which the origin should be shifted in order to eliminate x and y in the equation x2+y2+8x−6y+25=0 is
View SolutionThe point to which the origin should be shifted in order to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0 is
View SolutionThe point to which the origin should be shifted in order to eliminate x and y in terms in the equation x2−y2+2x+4y=0 is
View SolutionThe point to which the origin should be shifted in order to eliminate x and y terms in the equation 2x2−3y2−12x−6y+5=0 is
View SolutionThe point to which the origin should be shifted in order to eliminate x and y in the equation 2(x−5)2+3(y+7)2=10 is
View SolutionThe transformed equation of 4x2+9y2−8x+36y+4=0 when the axes are translated to the point (1,-2) is
View SolutionThe point to which the origin should be shifted in order to eliminate x and y terms in the equation x2+3y2−2x+12y+1=0 is
View SolutionFind the point to which the origin has to be shifted to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0
View SolutionFind the point to which the origin has to be shifted to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0
View Solution
