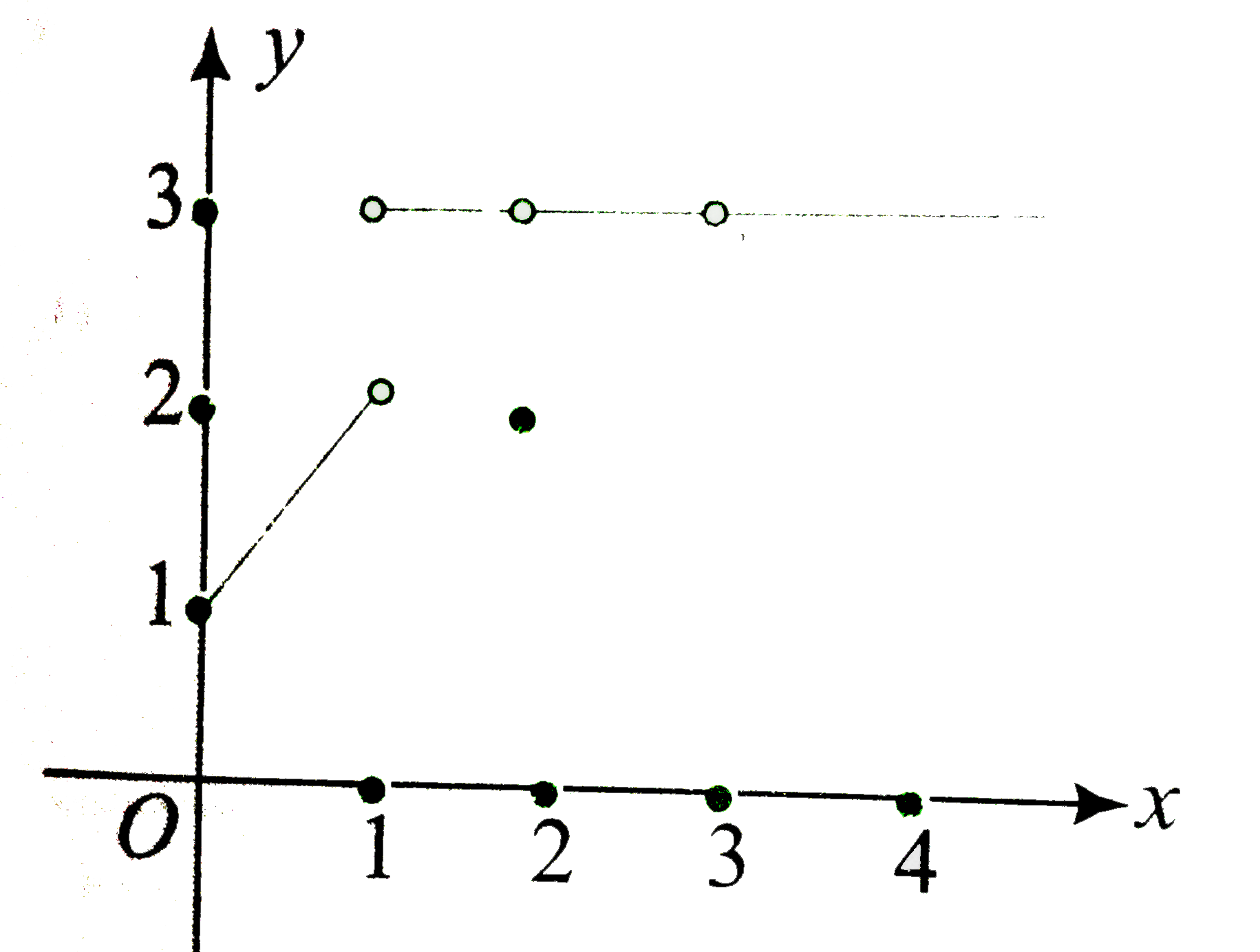
Sketch the graph of a function f that satisfies the given values:
f(-2) = 0 , f(2) = 0 , limx→−2f(x)=0
limx→2f(x) does not exist.Solution in Tamil
Step by step video & image solution for Sketch the graph of a function f that satisfies the given values: f(-2) = 0 , f(2) = 0 , lim_(xto-2)f(x)=0 lim_(xto2)f(x) does not exist. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - SURA PUBLICATIONCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.2
14 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - SURA PUBLICATIONCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.3
12 Videos
- COMBINATORICS AND MATHEMATICAL INDUCTION BOOK - SURA PUBLICATIONCHAPTER - COMBINATORICS AND MATHEMATICAL INDUCTION EXERCISE - ADDITIONAL PROBLEMS (section - D)
5 Videos
- DIFFERENTIAL CALCUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATIONBOOK - SURA PUBLICATIONCHAPTER - DIFFERENTIAL CALCUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATIONEXERCISE - ADDITIONAL PROBLEMS SECTION-D (5 MARKS)
4 Videos
Similar Questions
Solve : limx→2x4−16x−2
View SolutionFind the left and right limits of
f(x)=x2−4(x2+4x+4)(x+3) at x = -2
View SolutionFind the sum of all 4-digit numbers that can be formed using the digits 1,2,4,6 and 8.
View SolutionIf y=√1+ex1−ex, show that dydx=ex(1−ex)√1−e2x.
View SolutionGiven lim_(x rarr0)(f(x))/(x^(2))=2 then lim_(x rarr0)[f(x)]=
View SolutionIf a function satisfies the relation f(x)f''(x)−f(x)f'(x)=(f'(x))2∀x∈Randf(0)=f'(0)=1, then
The value of limx→−∞f(x) is
View Solutionयदि f एक निरंतर वर्धमान फलन है तब limx→0f(x2)−f(x)f(x)−f(0) का मान है :
View Solutionयदि f एक फलां इस प्रकार है कि f(−x)=−f(x) तथा limx→0f(x) का अस्तित्व है तब सिद्ध कीजिए कि limx→0f(x)=0
View SolutionIf limx→2f(x)−f(2)x−2 exist ,then
View SolutionSketch the graph of a function f that satisfies the given values:
f(0) is underfined limx→0f(x)=4,
f(2) = 6, limx→2f(x)=3
View SolutionStatement 1: If f(x)=2πcot−1(3x2+1(x−1)(x−2)), then limx→1−f(x)=0 and limx→2−f(x)=2
Statement 2: limx→∞cot−1x=0 and limx→−∞cot−1x=π
View SolutionSketch the graph of a function f that satifies the given values:
f(0) is undefined limx→0f(x)=4, f(2)=6 , limx→2f(x)=3
View SolutionSketch the graph of a function f that satifies the given values:
f(−2)=0 ,f(2)=0, limx→−2f(x)=0 , limx→2f(x) does not exist.
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?
(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.
View SolutionIf a function satisfies the relation f(x)f''(x)−f(x)f'(x)=(f'(x))2∀x∈Randf(0)=f'(0)=1, then
The value of limx→−∞f(x) is
View Solution
