If the potential energy of the particle is α−β2x2 then force experienced by the particle is
F=β2x2
F=βx
F=−βx
F=−β2x2
The correct Answer is:B
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - SURA PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - EXERCISE QUESTIONS (II. SHORT ANSWER QUESTIONS.)
8 Videos
- WORK, ENERGY AND POWER BOOK - SURA PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - EXERCISE QUESTIONS (III. LONG ANSWER QUESTIONS.)
6 Videos
- WAVES BOOK - SURA PUBLICATIONCHAPTER - WAVES EXERCISE - VALUE BASED QUESTIONS
2 Videos
Similar Questions
A particle of charge q and mass m moves rectilinearly under the action of an electric field E=α−βx. Here, αandβ are positive constants and x is the distance from the point where the particle was initially at rest. Then:
(1) the motion of the particle is oscillatory with amplitude αβ
(2) the mean position of the particles is at x=αβ
(3) the maximum acceleration of the particle is qαm
(4) All 1, 2 and 3
View SolutionPotential energy of a system of particles is U=α3r3−β2r2, where r is distance between the particles. Here αandβ are positive constants. Which of the following are correct for the system?
View Solution
Knowledge Check
Potential energy of a system of particles is Uα3r3−β2r2, where r is distance between the particles. Here αandβ are positive constants. Which of the following are correct for the system?
AEqulibrium separation between the particles is αβBFor r=αβ, the equlibrium is stableCFor r=αβ, the equlibrium is unstableDWork required to slowly move the particles to infinite separation from initial equlibrium position is βαThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
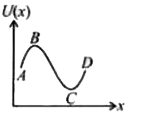 ACBBCB and CDA and D
ACBBCB and CDA and DThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
 ACBBCB and CDA and D.
ACBBCB and CDA and D.
The potential energy of a particle of mass 1 kg free to move along x-axis is given by U(x)=(x22−x) joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionThe potential energy of a particle of mass 2 kg in SHM is (9x2)J. Here x is the displacement from mean position . If total mechanical energy of the particle is 36 J. The maximum speed of the particle is
View SolutionA particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
View SolutionThe potential energy of a particle of mass 2 kg in SHM is (9x2)J. Here x is the displacement from mean position . If total mechanical energy of the particle is 36 J. The maximum speed of the particle is
View SolutionA particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
View Solution
