A piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg Solution in Tamil
Spring factor of liquid = Aρg
Inertia factor of wood piece = m
Time period T=2π√Inertia factorSpring factor
T=2π√mAρg
Topper's Solved these Questions
- BOOK - SURA PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - ADDITIONAL QUESTIONS (I MULTIPLE CHOICE QUESTIONS)20videos
OSCILLATIONS
- BOOK - SURA PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - ADDITIONAL QUESTIONS (III. FILL IN THE BLANKS)10videos
OSCILLATIONS
- BOOK - SURA PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - EXERCISE QUESTIONS (III. LONG ANSWER QUESTIONS)10videos
OSCILLATIONS
- BOOK - SURA PUBLICATIONCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - ADDITIONAL QUESTIONS241videos
NATURE OF PHYSICAL WORLD AND MEASUREMENT
- BOOK - SURA PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - Value based Questions5videos
PROPERTIES OF MATTER
Similar Questions
A Particle excites simple harmonic motion between x=−A&x=+A , the time taken for it to go from O to A2 is T1 & to go from A2 to A is T2 then
04:49View SolutionThe time period for U - tube Oscillation is ……….. .
07:14View SolutionWhat is meant by simple harmonic oscillation ? Give example
02:16View SolutionA substance whose mas is 4.27 g occupies 1.3cm3. The number of significant figure in density is
07:58View Solutionthe r.m.s. velocity of the molecules of a certain diatomic gas is found to be 1.6 Km/sec. the gas is
05:20View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
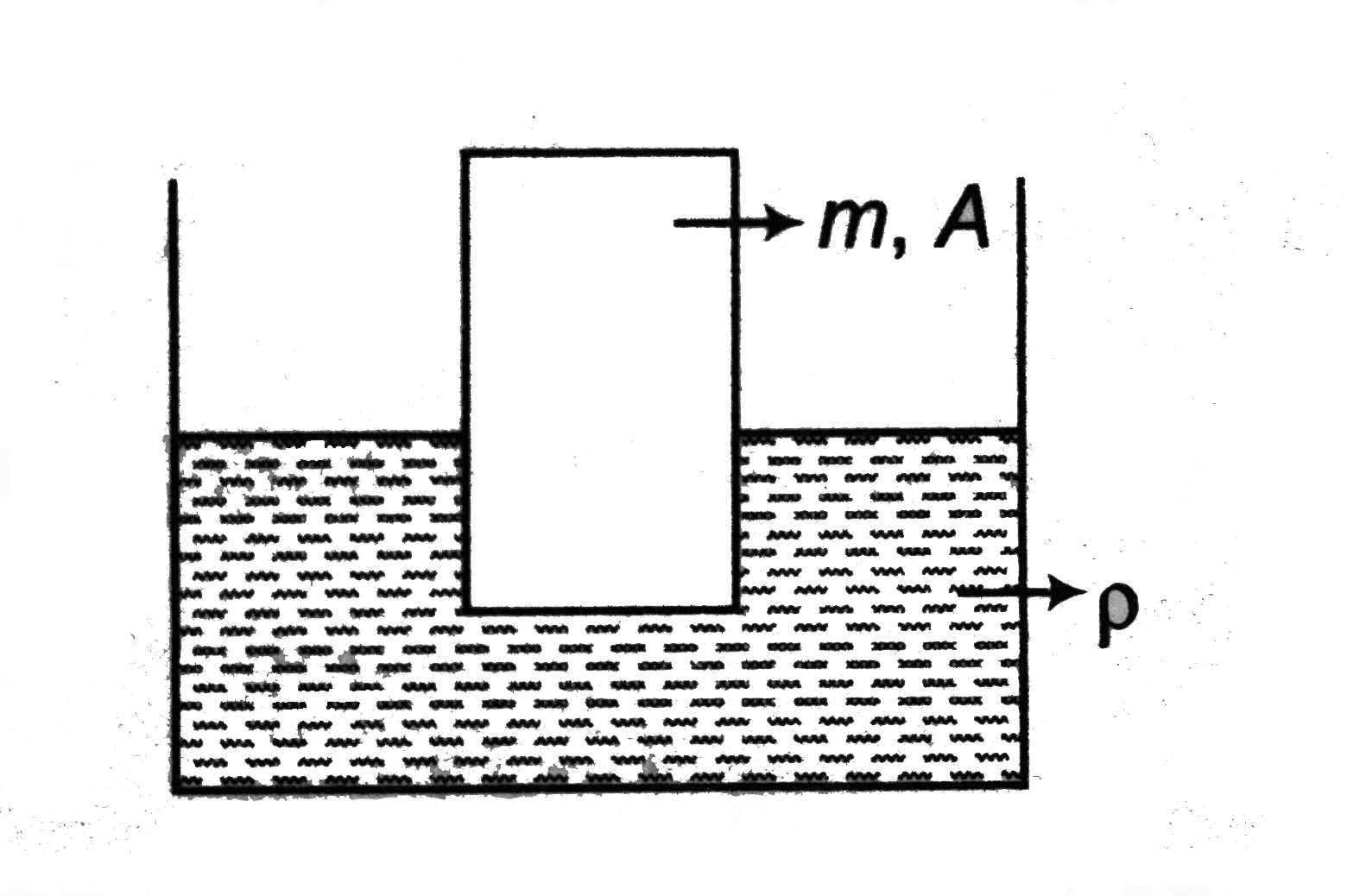 05:20View Solution
05:20View SolutionA cylinderical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a tiem period. T=2pisqrt((m)/(Arhog) where m is mass of the body and rho is density of the liquid.
05:20View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.03:57View SolutionA cylindrical piece of cork of density rho , base area A and height h, floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2pisqrt((hrho)/(rho_(1)g)) , where 'rho' is the density of the cork.
02:55View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
08:27View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).13:26View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View Solution

