You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A(4, -6), B(3, -2) and C(5, 2).Solution in Kannada
Step by step video & image solution for You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for Delta ABC whose vertices are A(4, -6), B(3, -2) and C(5, 2). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - SUBHASH PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 7.4
12 Videos
- COORDINATE GEOMETRYBOOK - SUBHASH PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 7.2
10 Videos
- CONSTRUCTIONSBOOK - SUBHASH PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 6.2
5 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - SUBHASH PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - EXERCISE 11.4 (PROVE THE FOLLOWING)
10 Videos
Similar Questions
Determine the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).

View SolutionFind the corrdinates of the point which divides the join of (-1, 7) and (4, -3) into the ratio 2 : 3 internally.
View SolutionDraw a circle a radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
View SolutionProve the following identities , where the angles involved are acute angles for which the expressions are defined.
(i) (cosecθ−cotθ)2=1−cosθ1+cosθ
View SolutionYou have studied in Class IX, (Chapter 9. Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ ABC whose vertices A(4, – 6), B(3, –2) and C(5, 2).
View SolutionIf A(4,−6),B(3,−2)andC(5,2) are the vertices of ABC, then verify the fact that a median of a triangle ABC divides it into two triangles of equal areas.
View SolutionIf A (1,2) , B(-2, 3) and C(-3,-4) be the vertices of ΔABC . Verify that median BE divides it into two triangles of equal areas.
View Solutionकक्षा IX में आपने पढ़ा है (अध्याय 9, उदाहरण 3) कि किसी त्रिभुज की एक माधियका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है | उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4,−6),B(3,−2) और C(5,2) हैं |
View SolutionA(7, -3), B(5, 3) and C(3, -1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
View Solutionआप जानते है कि किसी त्रिभुज कि एक माधियका उसे बराबर क्षेत्रफलों वालो दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिये जिसके शीर्ष A(4,−6),B(3,−2) और C(5,2) है।
View Solutionत्रिभुज कि मध्यिका त्रिभुज के क्षेत्रफल को दो समान भागो में बाटती है | इस कथन को ΔABC के लिए सत्यापित करे जिसके शीर्ष A(4,−6),B(3,−2) और C≡(5,2) है |
View Solutionयदि ΔABC के शीर्ष A(4,−6),B(3,−2) और C(5,2) हैं तो इस तथ्य को सत्यापित कीजिए कि त्रिभुज ABC की माध्यिका इसे दो बराबर क्षेत्रफलों वाले त्रिभुजों में विभाजित करती है ।
View Solutionयदि A(4, -6), B(3, -2) और C(5, 2) एक त्रिभुज ABC के शीर्ष तथा AD इसकी माध्यिका है, तो सिध्द कीजिए कि माध्यिका AD, ΔABC को बराबर क्षेत्रफल के दो त्रिभुजों में विभाजित करती है ।
View Solutionकक्षा IX में आपने पढ़ा है की किसी त्रिभुज की एक मध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है । उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, -6), B(3, -2) और C(5, 2) हैं ।
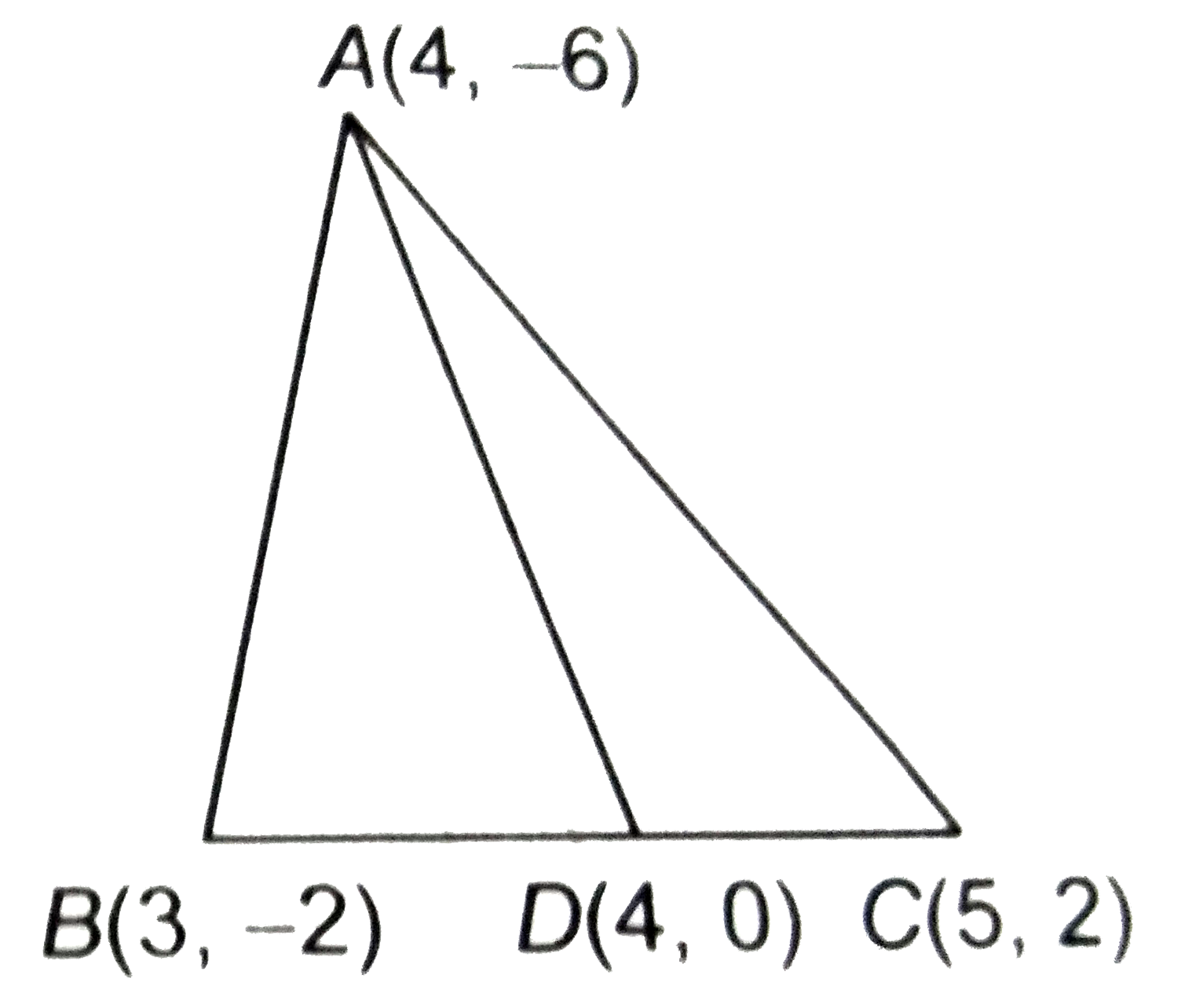
View SolutionYou have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A(4, -6), B(3, -2) and C(5, 2).
View SolutionVerify the Median of a triangle divides into two triangles of the equal whose vertices are A(4,-6),B(3,-2) and C(5,2)
View Solution
