If the n-th term of an arithmetic progression an = 24 - 3n, then its 2nd term is Solution in Kannada
18
15
0
2
The correct Answer is:A
Step by step video, text & image solution for If the n-th term of an arithmetic progression a_(n) = 24 - 3n, then its 2nd term is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - S.S.L.C ANNUAL EXAMINATION QUESTION PAPER MARCH- 2019 ( WITH ANSWERS )EXERCISE - II. Answer the following38videos
S.S.L.C ANNUAL EXAMINATION QUESTION PAPER MARCH- 2019 ( WITH ANSWERS )
- BOOK - SUBHASH PUBLICATIONCHAPTER - REAL NUMBEREXERCISE - EXERCISE 8.419videos
REAL NUMBER
- BOOK - SUBHASH PUBLICATIONCHAPTER - SOME APPLICATIONS OF TRIGONOMETRY EXERCISE - EXERCISE 9.116videos
SOME APPLICATIONS OF TRIGONOMETRY
Similar Questions
The given graph represents a pair of linear equations in two varibles . Write how many solutions these pair of equations have .
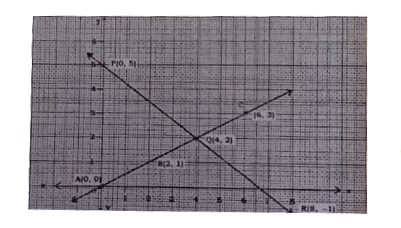 01:21View Solution
01:21View SolutionWithout actually performing the long division state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion
13312500:35View SolutionA circus artist is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground.Find the height of the pole, if the angle made by the rope with the ground levelis 30∘ ( see Figure)
01:18View SolutionWrite the common differnece of an Arithmetic Progression, whose nth term is given by tn=3n+7.
View SolutionIf the n-th term of an arithmetic progression is 5n+3, then 3rd term of the arithmetic progression is
02:40View SolutionIf the nth term of an arithmetic progression an=24−3n, then it's 2nd term is
06:46View SolutionThe sum of n terms of two arithmetic progressions are in the ratio (3n + 8) : (7n + 15). Find the ratio of their 12th terms.
05:31View SolutionThe sum of n terms of two arithmetic progressions are in the ratio (3n + 8) : (7n + 15). Find the ratio of their 12th terms.
01:07View SolutionThe sum of n terms of two arithmetic progressions are in the ratio (3n + 8) : (7n + 15). Find the ratio of their 12th terms.
04:30View SolutionThe sum of n terms of two arithmetic progressions are in the ratio (3n + 8) : (7n + 15). Find the ratio of their 12th terms.
02:10View SolutionIf the n−th term of an arithmetic progression an=24−3n then its 2nd term is
02:24View SolutionThe sum of n terms of two arithmetic progressions are in the ratio (3n+8):(7n+15). Find the ratio of their 12th terms.
05:00View SolutionThe n th term of a progression is 3n−5.Find its 15th term.
02:45View SolutionIn an arithmetic progression,if Sn=n(5+3n) and tn=32 ,then the value of n is
[Note: S(n) and t(n) denote the sum of first n terms and n th term of arithmetic progression respectively.]View SolutionThe sum of n terms of two arithmetic progressions are in the ratio (3n+8):(7n+15). Find the ratio of their 12th terms.
View Solution

