The seventh term of an arithmetic progression is four times itss second term and twelth term is 2 more than three times of its fourth term. Find the progression. Solution in Kannada
Step by step video & image solution for The seventh term of an arithmetic progression is four times itss second term and twelth term is 2 more than three times of its fourth term. Find the progression. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- S.S.L.C ANNUAL EXAMINATION QUESTION PAPER MARCH- 2019 ( WITH ANSWERS )BOOK - SUBHASH PUBLICATIONCHAPTER - S.S.L.C ANNUAL EXAMINATION QUESTION PAPER MARCH- 2019 ( WITH ANSWERS )EXERCISE - II. Answer the following
38 Videos
- REAL NUMBERBOOK - SUBHASH PUBLICATIONCHAPTER - REAL NUMBEREXERCISE - EXERCISE 8.4
19 Videos
- SOME APPLICATIONS OF TRIGONOMETRY BOOK - SUBHASH PUBLICATIONCHAPTER - SOME APPLICATIONS OF TRIGONOMETRY EXERCISE - EXERCISE 9.1
16 Videos
Similar Questions
The given graph represents a pair of linear equations in two varibles . Write how many solutions these pair of equations have .
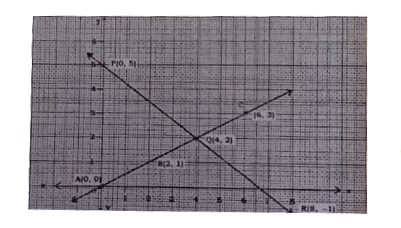
View SolutionWithout actually performing the long division state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion
133125
View SolutionA circus artist is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground.Find the height of the pole, if the angle made by the rope with the ground levelis 30∘ ( see Figure)
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometic progression colncide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe seventh term of an Arithmetic progression is four times its second term and twelfth term is 2 more than three times of its fourth term.Find the progression.
View SolutionIf seven times of 7th term of an Arithmetic Progression is euqal to the 11 times of 11th term of it, then find the 18th term of that Arithmetic Progression.
View SolutionThe sum o the fourth and eighth terms of arithmetic progression is 24 and the sum of the sixth and tenth terms is 44. Find the first three terms of the Arithmetic progression:
View SolutionIn an arithmetic progression sixth term is one more than twice the thrid term. Tha sum of the fourth and fifth terms is five times the secon term. Find the tenth term of the arithmatic progression.
View SolutionThe first, second and seventh terms of an arithmetic progression (all the terms are distinct) are in geometric progression and the sum of these three terms is 93. Then, the fourth term of this geometric progression is
View SolutionIn an arithmetic progression, thrice the second term is equivalent to eighth term and the sum of fourth term and the seventh term is 9 greater than the ninth term. Find the AP.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe third term of an arithmetical progression is 7, and the seventh term is 2 more than 3 times the third term. Find the first term, the common difference and the sum of the first 20 terms.
View SolutionThe first, second and seventh terms of an arithmetic progression (all the terms are distinct) are in geometric progression and the sum of these three terms is 93. Then, the fourth term of this geometric progression is
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View Solution
