One end of a thick copper rod is immersed into a steam chamber and the other end h:as metal coiled tube through which cold water at 15∘C is circulated. · If the length of the rod is 0.30 m, thickness 0.04 m, K of copper is 375 Wm−1K−1 and specific heat of water 4200 Jkg−1K−1, then calculate the final temperature of 0.10 kg of water at the end of 10 minutes, the temperatllre at the other end being 80∘C.Solution in Kannada
K=375Wm−1K−1,t=10×60=60s
A=3.142×(0.04)24=12.56×10−4m2
d=0.30m,θ1=100∘C,θ2=80∘C,θ3=15∘C,θ4=?
Applying Q=KA(θ1−θ2)td=ms(θ4−θ3)
θ4−θ3=KA(θ1θ2)tmsd,θ1−θ2=100−80=20∘C
=375×12.568×10−4×20×6000.1×4200×0.30=565.56126
θ4−θ3=4.49∘C
hence θ4=θ3+4.49∘=15+4.49∘
θ4=19.49∘C
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - THREE MARKS QUESTIONS AND ANSWERS12videos
THERMAL PROPERTIES OF MATTER
- BOOK - SUBHASH PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NUMERICAL WITH SOLUTIONS34videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - SUBHASH PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - NUMERICALS WITH SOLUTIONS24videos
THERMODYNAMICS
Similar Questions
Explain anomalous expansion of water
03:00View SolutionA non-uniform bar of weight 'w' is suspended at rest by two strings of negligible weight. The angles made by the strings with the vertical are 36.9∘ and 53.1∘C respectively. The bar is 2m long. Calculate the distance 'd' of the centre of gravity of the bar from its left. (refer fig).-NCERT
 03:28View Solution
03:28View SolutionA refrigerator is used to mainatain eatables kept inside it at 9∘C. If the room temperature is 35∘C, then calculate the coefficient to performance. Calculate the amount of heat rejected to the surrounding.
02:35View SolutionCertain amount of heat is given to 100 g of copper to increase its temperature by 21^@C . If same amount of heat is given to 50 g of water, then the rise in its temperature is (specific heat capacity of copper = 400 J kg^(-1) K^(-1) and that for water = 4200 J kg^(-1) K^(-1))
07:22View SolutionWhat is the temperature of the steel-copper junction in the steady state system show in Fig. 7(e).17? Length of steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =300∘C, temperature of other end 0∘C. The are of cross-section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2js−1m−1K−1 and of copper =3895js−1m−1K−1).
 03:42View Solution
03:42View SolutionWhat is the temperature of the steel -copper junction in the steady state of the system shown in the figure. Length of the steel rod =25cm , length of the copper rod =50cm , temperature of the furance =300^(@)C , temperature of the other end =0^(@)C . The area of cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50Js^(-1)m^(-1)K^(-1) and of copper =400 J s^(-1)m^(-1)K^(-1) )
04:23View SolutionA cylindrical steel rod of length 0.10 m and thermal conductivity 50 W.m^(-1) K^(-1) is welded end to end to copper rod of thermal conductivity 400 W.m^(-1). K^(-1) and of the same area of cross section but 0.20 m long. The free end of the steel rod is maintained at 100^(@)C and that of the copper and at 0^(@)C . Assuming that the rods are perfectly insulated from the surrounding, the temperature at the junction of the two rods–
08:21View Solutionthe thermal capacity of 11 kg of water is same as 120 kg of copper. If specific heat capacity of water is 4200. J kg−1 K−1, find the specific heat capacity of copper.
07:19View Solutionचित्र 11.15 में दर्शाए गए निकाय की स्थाई अवस्था में स्टील - ताँबा संधि का ताप क्या है ? स्टील छड़ की लंबाई = 15.0 cm, ताँबे की छड़ की लंबाई = 10.0 cm, भट्ठी का ताप = 300∘C, दुसरे सिरे का ताप = 0∘C , स्टील की छड़ की अनुप्रस्थ काट के क्षेत्रफल ताँबे की छड़ की अनुप्रस्थ काट के क्षेत्रफल का दो गुना है | (स्टील की ऊष्मा चालकता = 50.2 J s−1m−1K−1, ताँबे की ऊष्मा चालकता = 385Js−1m−1K−1)
02:45View SolutionA uniform copper rod 50 cm long is insulated on the sides, and has its ends exposed to ice and steam, respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.
02:15View Solutionचित्र में दर्शाये गये निकाय की स्थायी अवस्था में स्टील तांबा संधि का माप क्या है? स्टील छड़ की लम्बाई =15.0cm तांबे की छड़ की लम्बाई =10.0cm भट्टी का ताप =300∘C, दूसरे सिरे का ताप =0∘C, स्टील की छा़ की अनुप्रस्थ काट का क्षेत्रफल तांबे की छड़ की अनुप्रस्थ काट के क्षेत्रफल का दोगुना है। स्टील की ऊष्मा चालकता =50.2JS−1m−1K−1, तांबे की ऊष्मा चालकता =385JS−1m−1K−1
 06:21View Solution
06:21View SolutionCalculate the heat energy required to raise the temperature of 2 kg of water from 10^@C to 50^@C . Specific heat capacity of water is 4200 JKg^(-1) K^(-1)
04:02View SolutionWhat is the temperature of the steel - copper junction in the steady state of the system shown in Fig. Length of the steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =400" "^(@)C , temperature of the other end =0" "^(@)C . The area of cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2" J s"^(-1)m^(-1)K^(-1), and of copper =385" J s"^(-1)m-1" "K^(-1) ).
02:54View SolutionOne end of a uniform rod of length 1 m is placed in boiling water while its other end is placed in melting ice. A point P on the rod is maintained at a constant temperature of 800^(0)C . The mass of steam produced per seecond is equal to the mass of ice melted per second. If specific latent heat of steam is 7 times the specific latent heat of ice. Then the distance .p. form the steam chamber is (1)/(K) . The value of K = ______________
03:27View SolutionWhat is the temperature of the steel - copper junction in the steady state of the system shown in Fig.11.15.
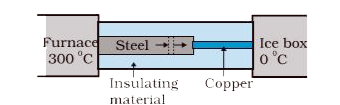
Length of the steel rod =15.0cm, length of the copper reod =10.0 cm, temperarure of the furnace =300∘C, temperature of the furnace =300∘C , temperature of the other end =0∘C. The are of cross section of the steel rod is twice that of the copper rod. ( Thermal conductivity of steel =50.2Js−1m−1K−1, and of copper =385Js−1m−1K−1).04:34View Solution

