One end of a long string of linear mass density is connected to an electrically driven tuning fork of frequency 256 Hz. The other passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude . At t=0, the left end ( fork end) of the string x = 0 has zero transverse displacement ( y = 0 ) and is moving along positive y - direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as a function of x and t that describe the wave on the string. Solution in Kannada
Amplitude A = 0.05m, mass = 90 kg
frequency f = 256 Hz, linear density =
Velocity of the wave
Wavelength
i.e.
Propagation constant
angular frequency
epoch
Standard equation for a wave travelling along ve direction with R = 0, t = 0
i.e., .
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - WAVESEXERCISE - FIVE MARKS QUESTIONS WITH ANSWERS11videos
WAVES
- BOOK - SUBHASH PUBLICATIONCHAPTER - UNITS AND MEASUREMENTS EXERCISE - NUMERICALS WITH SOLUTIONS13videos
UNITS AND MEASUREMENTS
- BOOK - SUBHASH PUBLICATIONCHAPTER - WORK, POWER AND ENERGY EXERCISE - NUMERICALS WITH SOLUTIONS33videos
WORK, POWER AND ENERGY
Similar Questions
Show that the distance between any two consecutive nodes or antinodes in a stationary wave is λ/2.
View SolutionThe period of oscillation (T) of a simple pendulum depends on the probable quantities such as mass 'm' of a bob, length 'l' of the pendulum and acceleration due to gravity 'g' at the place. Derive an equation using dimensional analysis.
06:44View SolutionThe K.E. of electron is 10 keV. Calculate its speed.
03:43View SolutionOne end of a long string of linear mass density 10^(-2) kg m^(-1) is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
03:11View SolutionOne end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
07:49View SolutionThe linear mass density of the string shown in the figure is mu = 1 g//m . One end (A) of the string is tied to a prong of a tuning fork and the other end carries a block of mass M. The length of the string between the tuning fork and the pulley is L = 2.0 m . When the tuning fork vibrates, the string resonates with it when mass M is either 16 kg or 25 kg. However, standing waves are not observed for any other value of M lying between 16 kg and 25 kg. Assume that end A of the string is practically at rest and calculate the frequency of the fork.
04:49View SolutionA light string passes over a frictionless pulley. To one of its ends a mass of 6 kg is attached. To its other end a mass of 10 kg is attached. The tension in the thread will be
 View Solution
View Solution8.0×10−3 kg m 1 रैखिक द्रव्यमान घनत्व की किसी लंबी डोरी का एक सिरा ( 256 Hz आवृत्ति के विद्युत चालित स्वरित्र द्विभुज से जुड़ा है । डोरी का दूसरा सिरा किसी स्थिर घिरनी के ऊपर गुजरता हुआ किसी तुला के पलड़े से बंधा है जिस पर 90 kg के बाट लटके है । घिरनी वाला सिरा सारी आवक ऊर्जा को अवशोषित कर लेता है जिसके कारण इस सिरे से परावर्तित तरंगो का आयाम नगण्य होता है । t=0 पर डोरी के बाएं सिरे (द्विभुज वाले सिरे ) x=0 पर अनुप्रस्थ विस्थापन शून्य है y=0 तथा वह y की धनात्मक दिशा के अनुदिश गतिशील है । तरंग का आयाम 5.0 cm है । डोरी पर इस तरंग का वर्णन करने वाले अनुप्रस्थ विस्थापन y को x तथा t के फलन के रूप में लिखिए ।
02:26View Solution8.0×10−3किग्रा/मीटर रैखिक द्रव्यमान घनत्व की किसी लम्बी डोरी एक सिरा 256 Hz आवृत्ति के विधुत चालित स्वरित्र माध्यम द्विभुज से ऊपर गुजरता हुआ किसी तुला के पलड़े से बंधा है जिस पर किग्रा के बाँट लटके हैं । घिरनी वाला सिरा सारी आवश्यक ऊर्जाको अवशोषित कर लेता है जिसके कारण इस सिरे से परावर्तित तरंगों का आयाम नगण्य होता है | t=0 पर डोरी के बायें सिरे (द्विभुज वाले सिरे) x=0 पर अनुप्रस्थ विस्थापन शून्य है (y=0)तथा वह y की धनात्मक दिशाके अनुदिश गतिशील है । तरंग का आयाम 5.0 सेमी है डोरी पर इस तरंग का वर्णन करने वाले अनुप्रस्थ विस्थापन y को xतथाt के फलन के रूप में लिखिए ।
View SolutionOne end of a long string of linear mass density 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the leftend ( fork end )of the string x=0 has zero transverse displacement ( y = 0 ) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm.Write down the transverse displacement y as function of x and t that describes the wave on the string.
06:40View SolutionOne end of string which passes through pulley and connected to 10 kg mass at other end is pulled by 100 N force. Find out the acceleration of 10 kg mass. (g=9.8m/s2)
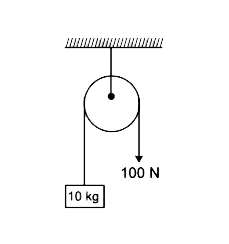 View Solution
View SolutionOne end of a long string of linear mass density 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.
07:27View SolutionOne end of a long string of linear mass density 8.0 xx 10^(-3) kg m^(-1) is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.
View SolutionOne end of a long string of linear mass density 8.0 xx 10^(-3) kg m^(-1) is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.
06:40View SolutionOne end of a long string of linear mass density 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.
05:17View Solution
