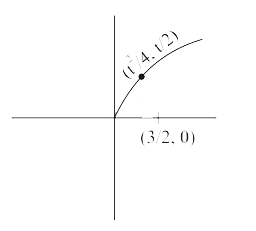
The shortest distance between the point $(\frac{3}{2}, 0)$ and the curve $y = \sqrt{x}, (x > 0)$ , is $\frac{\sqrt{k}}{2}$ . The value of k is ___________.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:5

The point located nearest to the given point must be the point common to the parabola and the normal passing through $(\frac{3}{2}, 0)$ .
$\frac{\frac{t}{2}}{\frac{t^{2}}{4} - \frac{3}{2}} = - t$
$\frac{2 t}{t^{2} - 6} + t = 0$
$t (\frac{2}{t^{2} - 6} + 1) = 0$
$t^{2} - 6 = - 2$
$t^{2} = 4$
$t = 2$ $(t > 0)$
Point (1,1)
Distance $= \sqrt{{(1 - \frac{3}{2})}^{2} + 1} = \frac{\sqrt{5}}{2}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
The shortest distance between the point $(\frac{3}{2}, 0)$ and the curve $y = \sqrt{x}, (x > 0)$ , is
A $\frac{3}{2}$
B $\frac{5}{4}$
C $\frac{\sqrt{3}}{2}$
D $\frac{\sqrt{5}}{2}$
Question 2 - Select One
The shortest distance between the point $(0, \frac{1}{2})$ and the curve $x = \sqrt{y}, (y > 0)$ , is:
A $\frac{3}{2}$
B $\frac{\sqrt{5}}{2}$
C $\frac{\sqrt{3}}{2}$
D $\frac{1}{2}$
Question 3 - Select One
The shortest distance between the line $y = x$ and the curve $y^{2} = x - 2$ is:
A2
B $\frac{7}{8}$
C $\frac{7}{4 \sqrt{2}}$
D $\frac{11}{4 \sqrt{2}}$

Recommended Questions

Home
Ask Doubt
Profile