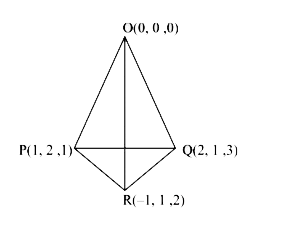
A tetrahedron has vertices $P (1, 2, 1), Q (2, 1, 3), R (- 1, 1, 2) and O (0, 0, 0)$ . The angle beween the faces OPQ and PQR is :

${cos}^{- 1} (\frac{9}{35})$

${cos}^{- 1} (\frac{17}{31})$

${cos}^{- 1} (\frac{7}{31})$

${cos}^{- 1} (\frac{19}{35})$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

A tetrahedron has vertices $P (1, 2, 1), Q (2, 1, 3), R (- 1, 1, 2) and O (0, 0, 0)$ . The angle beween the faces OPQ and PQR is :
A ${cos}^{- 1} (\frac{19}{35})$
B ${cos}^{- 1} (\frac{17}{31})$
C $30^{\circ}$
D $90^{\circ}$
For any four points O(0,0,0),P(1,2,1),Q(2,3,0),R(0,1,-1), the angle between the planes OPQ and PQR is
A ${cos}^{- 1} (\frac{5}{\sqrt{28}})$
B ${sin}^{- 1} (\frac{5}{\sqrt{28}})$
C ${cos}^{- 1} (\frac{5}{\sqrt{14}})$
D ${sin}^{- 1} (\frac{5}{\sqrt{14}})$
If $P (0, 1, 2), Q (4, - 2, 1)$ and $O (0, 0, 0)$ are three points, then $∠ P O Q =$
A $\frac{π}{6}$
B $\frac{π}{4}$
C $\frac{π}{3}$
D $\frac{π}{2}$