A positive point charge is released from rest at a distance r0 from a positive line charge with uniform density. The speed (v) of the point charge, as a function of instantaneous distance r from line charge, is proportional to:
v∝e+r/r0
v∝ln(rr0)
v∝√ln(rr0)
v∝(rr0)
The correct Answer is:c
E∝1r,F∝1r
a∝1r,vdv∝1rdr
v2∝ln(rr0),v∝√ln(rr0)
Similar Questions
A positive point charge is released from rest at a distance r0 from a positive line charge with uniform density. The speed (v) of the point charge, as a function of instantaneous distance r from line charge, is proportional to:

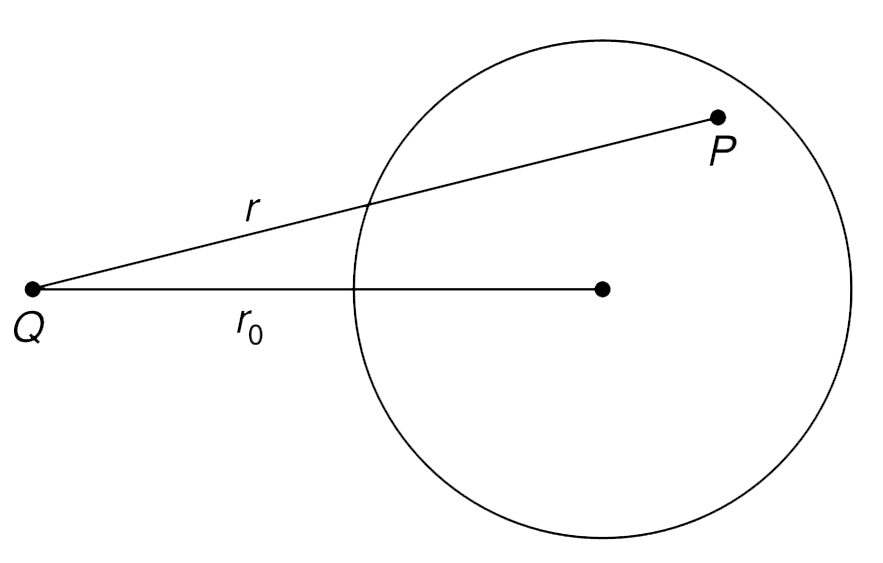
View SolutionA conducting shell having no charge has radius R. A point charge Q is placed in front of it at a distance r0 from its centre. Find potential due to charge induced on the surface of the shell at a point P inside the shell. Distance of point P from point charge Q is r.
View Solution
Knowledge Check
A positive charge released from rest:
Amoves towards the regions of lower potentialBmoves towards the regions of higher potentialCmoves towards the regions of equal potentialDdoes not moveThe electric field created by a point charge falls with distance r from the point charge as
A1rB1r2C1r3D1r4For a long wire of charge density γ,, field at a distance r from the wire is
Aγ2πε0rnBγ4πε0rnC0Dkqεe
A proton is fixed at origin. Another proton is released from rest, from a point at a distance r from origin. Taking charge of portion as e and mass as m, find the speed of the proton (i) at a distance 2r from origin (ii) at large distance from origin.

View Solution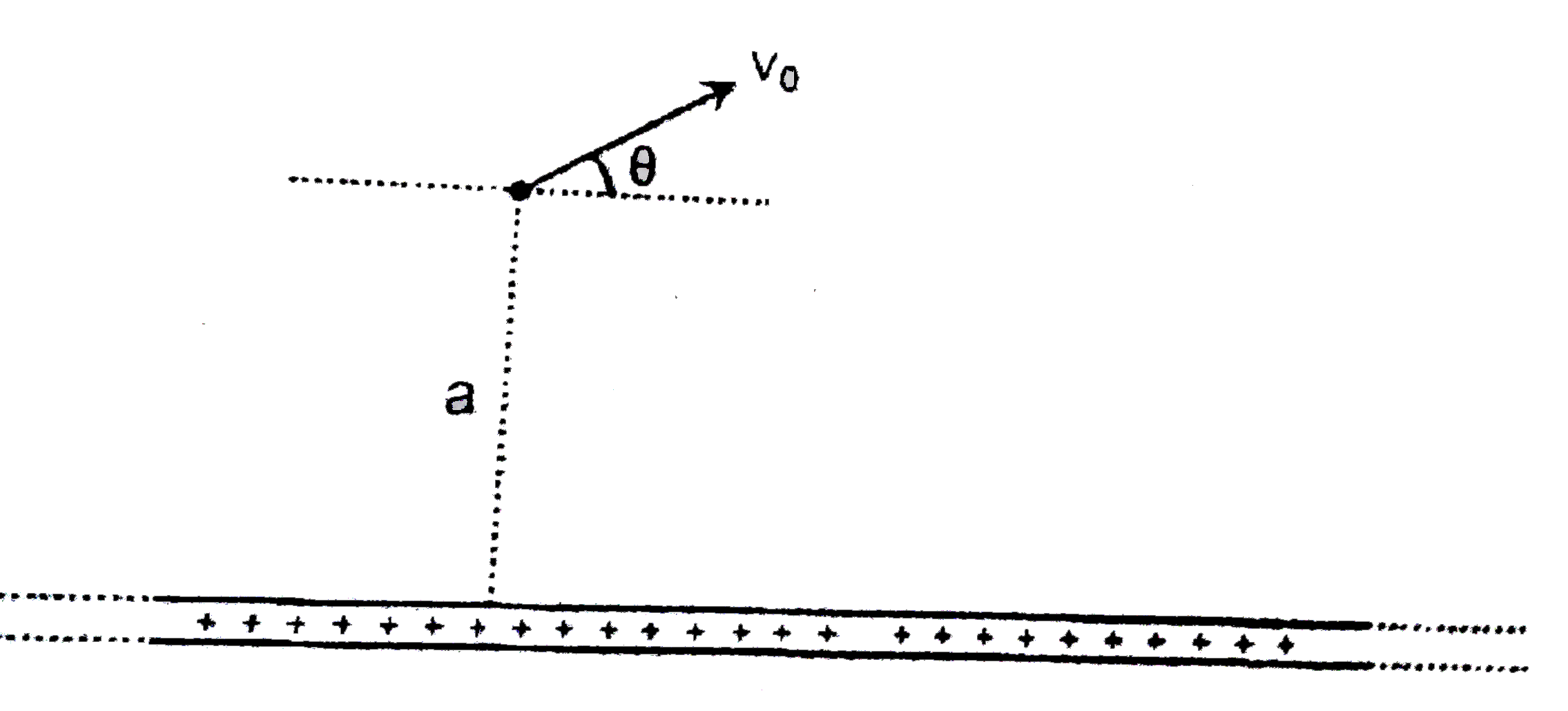
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε200/qλ). The value of n is (ingnore gravity)
View SolutionA point charge q is located at a distance l from an infinite conduting plane. Determine the surface density of charges induced on the plane as a function of separaction r from the base of the perpendicular drawn to the plane from the chagre.
View SolutionA positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to induced charge has magnitude
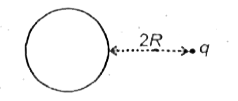
View SolutionA point P is at a distance r from a point charge q. if at point P, the electric potential is 300 V, and the electric field intensity is 75 V/m, then the distance of P from the point charge is
View Solution
