A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this square loop is changed to a circular loop and it carries the current, the magnitude of the magnetic dipole moment of circular loop will be :
4mπ
2mπ
3mπ
mπ
The correct Answer is:A
To solve the problem, we need to find the magnetic dipole moment of a circular loop when it is transformed from a square loop that carries a steady current I and has a magnetic dipole moment m.
1. Understanding the Magnetic Dipole Moment:
The magnetic dipole moment m for a current-carrying loop is given by the formula:
m=n⋅I⋅A
where n is the number of turns (which is 1 for a single loop), I is the current, and A is the area of the loop.
2. Area of the Square Loop:
For a square loop with side length a, the area A is:
Asquare=a2
Therefore, the magnetic dipole moment of the square loop is:
msquare=I⋅a2
Given that this is equal to m, we have:
m=I⋅a2
3. Circumference of the Square Loop:
The perimeter of the square loop is:
Psquare=4a
4. Finding the Radius of the Circular Loop:
When the square loop is transformed into a circular loop, the circumference of the circular loop is equal to the perimeter of the square loop:
2πr=4a
Solving for r:
r=4a2π=2aπ
5. Area of the Circular Loop:
The area A of the circular loop is given by:
Acircle=πr2
Substituting r:
Acircle=π(2aπ)2=π⋅4a2π2=4a2π
6. Magnetic Dipole Moment of the Circular Loop:
Now, substituting the area of the circular loop into the magnetic dipole moment formula:
mcircle=I⋅Acircle=I⋅4a2π
Since m=I⋅a2, we can express mcircle in terms of m:
mcircle=4π⋅m
Final Result:
Thus, the magnitude of the magnetic dipole moment of the circular loop is:
mcircle=4mπ
The magnetic dipole moment m for a current-carrying loop is given by the formula:
m=n⋅I⋅A
where n is the number of turns (which is 1 for a single loop), I is the current, and A is the area of the loop.
For a square loop with side length a, the area A is:
Asquare=a2
Therefore, the magnetic dipole moment of the square loop is:
msquare=I⋅a2
Given that this is equal to m, we have:
m=I⋅a2
The perimeter of the square loop is:
Psquare=4a
When the square loop is transformed into a circular loop, the circumference of the circular loop is equal to the perimeter of the square loop:
2πr=4a
Solving for r:
r=4a2π=2aπ
The area A of the circular loop is given by:
Acircle=πr2
Substituting r:
Acircle=π(2aπ)2=π⋅4a2π2=4a2π
Now, substituting the area of the circular loop into the magnetic dipole moment formula:
mcircle=I⋅Acircle=I⋅4a2π
Since m=I⋅a2, we can express mcircle in terms of m:
mcircle=4π⋅m
Thus, the magnitude of the magnetic dipole moment of the circular loop is:
mcircle=4mπ
Similar Questions
A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m.If this square loop is changed to a circular loop and it carries the same current the magnitude of the magnetic dipole moment of circular loop will be
View SolutionThe magnitude off magnetic moment of the current loop in the figure is

View Solution
Knowledge Check
Magnetic dipole moment of rectangular loop is
Ainversely proportional to current in loopBinversely proportional to area of loopCparallel to plane of loop and proportional to area of loopDperpendicular to plane of loop and proportional to area of loopThe magnetic dipole moment of current loop is independent of
Anumber of turnsBarea of loopCcurrent in the loopDmasgnetic field in which it is lyingThe magnitude of magnetic moment of the current loop in the figure is
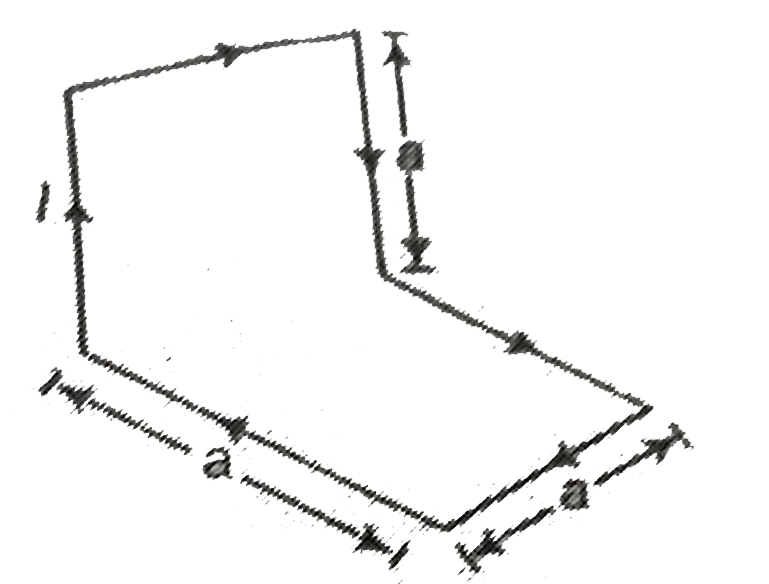 Ala2B√2la2CzeroDnone of the above
Ala2B√2la2CzeroDnone of the above
A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionThe magnetic dipole moment of a current loop is independent of
View SolutionA circular coil of radius r carries I. If the same coil is now changed into a square loop carrying the same current, magnitude of its magnetic moment will
View SolutionA circular loop of radius 0.05 m carries a current of 1.0 A. The magnetic moment of the loop is .
View SolutionA circular loop of radius0.05 m carriess a current of 1.0 A. The magnetic moment of the loop is .
View Solution
