An element has a face-centred cubic (fcc) structure with a cell edge of a. The distance between the centres of two nearest tetrahedral voids in the lattice is:

A

$\sqrt{2} a$

B

$\frac{a}{2}$

C

a

D

$\frac{3}{2} a$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$cos θ = \frac{1}{\sqrt{3}}$
The distance of corner atom to teat heel a void along diagonal $= \frac{\sqrt{3} a}{4}$

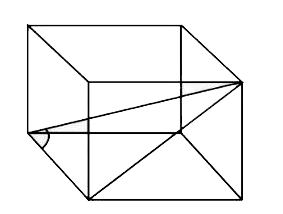
Component along any side $= \frac{\sqrt{3} a}{4} \times \frac{1}{\sqrt{3}} = \frac{a}{4}$
$(a - \frac{a}{4} + \frac{a}{4}) = \frac{a}{2}$

|

Updated on:21/07/2023

Class 12 CHEMISTRY QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
The minimum distance between an octahedral and a tetrahedral void in fcc lattice is
A $a \sqrt{3}$
B $\frac{a \sqrt{3}}{2}$
C $\frac{a \sqrt{3}}{3}$
D $\frac{a \sqrt{3}}{4}$
Question 2 - Select One
The distance between an ocatahral and tetrahedral void in fcc lattice would be:
A $\sqrt{3} a$
B $\frac{\sqrt{3 a}}{2}$
C $\frac{\sqrt{3 a}}{3}$
D $\frac{\sqrt{3 a}}{4}$
Question 3 - Select One
An example of a face centred cubic lattice is
AZinc
BSodium
CCopper
DCalcium chloride

Recommended Questions

Home
Ask Doubt
Profile