Complete removal of both the axial ligands (along the z-axis) from an octahedral complex leads to which of the following splitting patterns? (relative orbital energies not on scale).
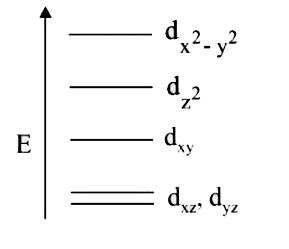
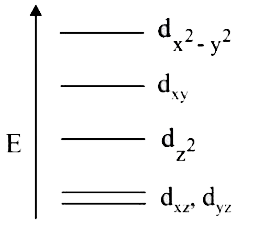
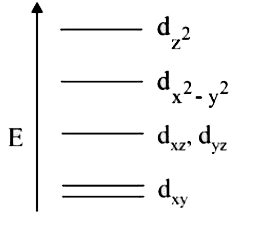
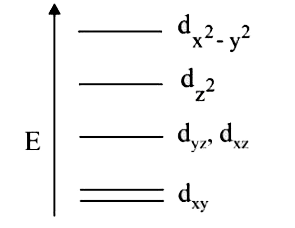
The correct Answer is:B
To solve the problem of determining the splitting pattern when both axial ligands are removed from an octahedral complex, we can follow these steps:
Step 1: Understand the Octahedral Complex
An octahedral complex has six ligands positioned at the vertices of an octahedron around a central metal ion. The ligands are typically arranged along the x, y, and z axes.
Step 2: Identify the Axial and Equatorial Ligands
In an octahedral complex:
- The axial ligands are located along the z-axis (above and below the central metal ion).
- The equatorial ligands are located in the xy-plane.
Step 3: Remove the Axial Ligands
When we completely remove both axial ligands from the octahedral complex, we are left with only the equatorial ligands. This transforms the complex from an octahedral geometry to a square planar geometry.
Step 4: Analyze the Splitting of d-Orbitals
In a square planar complex, the d-orbitals split differently compared to an octahedral complex. The relevant d-orbitals are:
- dxy: This orbital lies in the xy-plane and is stabilized due to the presence of ligands in the same plane.
- dx2-y2: This orbital is also in the xy-plane but has lobes that point directly towards the ligands, leading to increased repulsion and higher energy.
- dz2: This orbital is oriented along the z-axis and is less affected by the ligands in the xy-plane.
Step 5: Determine the Energy Levels
In a square planar arrangement, the order of energy levels for the d-orbitals is typically:
1. dx2-y2 (highest energy due to direct overlap with ligands)
2. dxy (lower energy due to being in the plane of the ligands)
3. dz2 (lowest energy as it is perpendicular to the plane of ligands)
Conclusion
Thus, the removal of both axial ligands leads to a square planar geometry with a specific splitting pattern of the d-orbitals. The energy levels are rearranged as follows: dx2-y2 > dxy > dz2.
Final Answer
The splitting pattern after the removal of both axial ligands from an octahedral complex results in the following order of d-orbital energies:
- dx2-y2 > dxy > dz2
---
An octahedral complex has six ligands positioned at the vertices of an octahedron around a central metal ion. The ligands are typically arranged along the x, y, and z axes.
In an octahedral complex:
- The axial ligands are located along the z-axis (above and below the central metal ion).
- The equatorial ligands are located in the xy-plane.
When we completely remove both axial ligands from the octahedral complex, we are left with only the equatorial ligands. This transforms the complex from an octahedral geometry to a square planar geometry.
In a square planar complex, the d-orbitals split differently compared to an octahedral complex. The relevant d-orbitals are:
- dxy: This orbital lies in the xy-plane and is stabilized due to the presence of ligands in the same plane.
- dx2-y2: This orbital is also in the xy-plane but has lobes that point directly towards the ligands, leading to increased repulsion and higher energy.
- dz2: This orbital is oriented along the z-axis and is less affected by the ligands in the xy-plane.
In a square planar arrangement, the order of energy levels for the d-orbitals is typically:
1. dx2-y2 (highest energy due to direct overlap with ligands)
2. dxy (lower energy due to being in the plane of the ligands)
3. dz2 (lowest energy as it is perpendicular to the plane of ligands)
Thus, the removal of both axial ligands leads to a square planar geometry with a specific splitting pattern of the d-orbitals. The energy levels are rearranged as follows: dx2-y2 > dxy > dz2.
The splitting pattern after the removal of both axial ligands from an octahedral complex results in the following order of d-orbital energies:
- dx2-y2 > dxy > dz2
Similar Questions
The splitting diagram for square planar complexes is more complex than for octahedral and tetrahedral complexes and is shown below with the relative energies of each orbital.
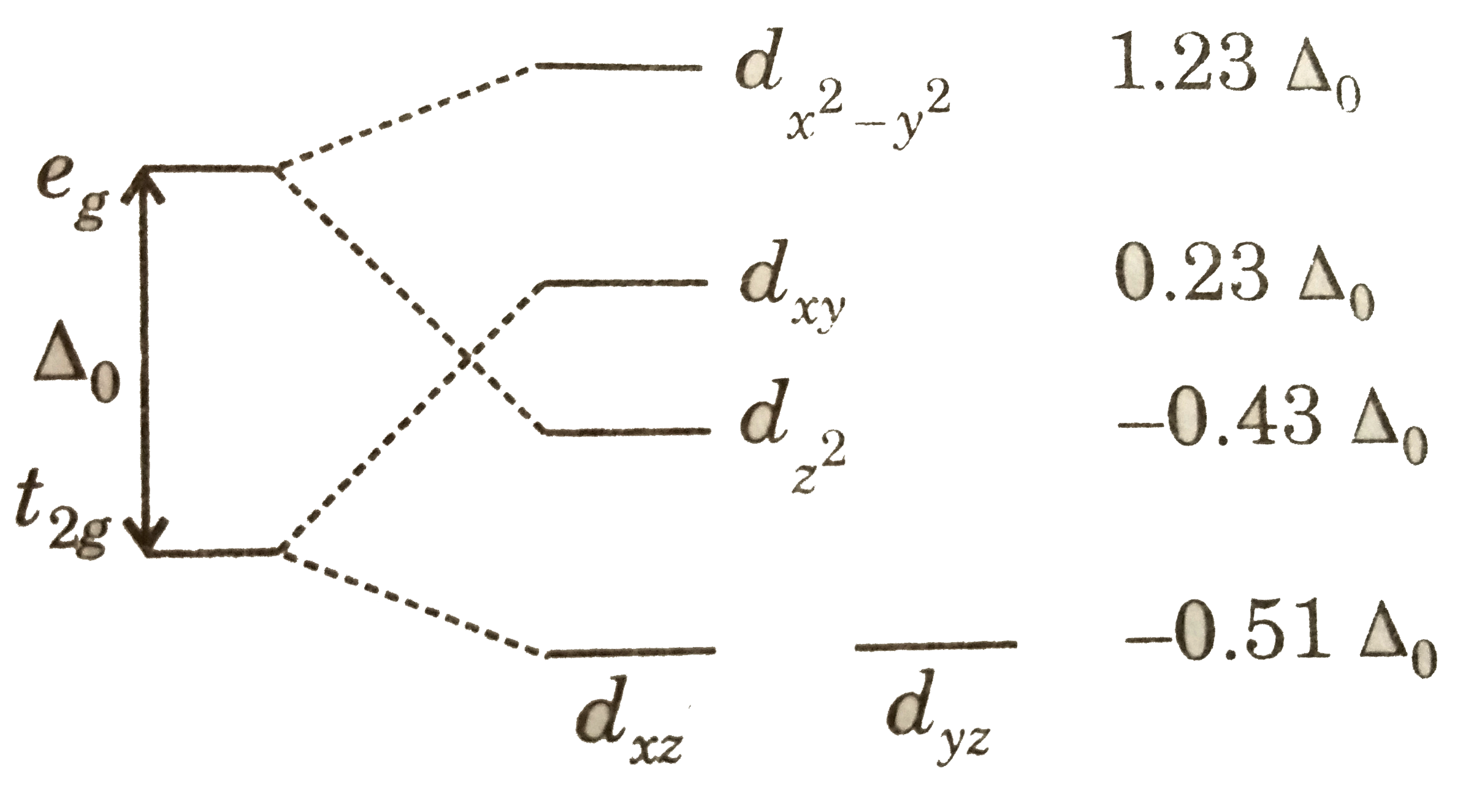
Calculate crystal field stabilisation energy for a diamagnetic square planar d8 metal complex with the help of above diagram neglecting pairing energy (P)View SolutionWhen degenerate d-orbitals of an isolated atom/ion come under influence of magnetic field of ligands, the degeneray is lost. The two set t2g(dxy,dyz,dxz)andeg(dx2−dx2−y2 are either stabilized or destabilized depending upon the nature of magnetic field. it can be expressed diagrammatically as:
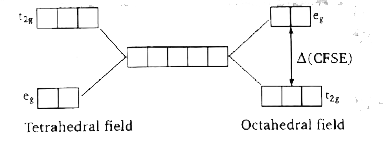
Value of CFSE depends upon nature of ligand and a spectrochemical series has been made experimentally, for tetrahedral complexes, Δ is about 4/9 times to Δ0 (CFSE for octahedral complex). this energy lies in visible region and i.e., why electronic transition are responsible for colour. such transition are not possible with d0andd10 configuration.
Q. For an octahedral complex, which of the followin d-electron configuration will give maximum CFSE?View Solution
Knowledge Check
- Question 1 - Select One
in which of the following change both the electrons are removed from same orbital ?
ACu→Cu+2+2e−BCr→Cr+2+2e−CGe→Ge+2+2e−DZn→Zn+2+2e− - Question 2 - Select One
In the octahedral crystal field, there is splitting of d orbitals. Which of the following d orbitals constitute the higher energy eg set of orbitals.
Adxy,dxyBdz2,dyzCdxy,dx2−y2Ddx2−y2,dz2 - Question 3 - Select One
According to cystal field theory, interaction between central metal atom/ion and ligand is electrostatic in nature. In free metal ions, the five d-orbitals are degenerate. However, in a ligand field e.g., tetrahedral, octahedral, square planar, square pyramidal, trigonal bipyramidal, the degeneracy of 5d-orbitals is lost.
If lobes of d-orbitals of central metal atom/ion are along the axes through which ligands are approaching, the energy of corresponding d-orbital is raised more than the d-orbitals having lobes between teh axes. e.g., octahedral complexes, square planar complexes, square pyramidal compexes.
Which of the following orbitals has the highest energy in square pyramidal ligand field ?AdxyBdz2Cdx2−y2Ddyz,d(zx)
According to cystal field theory, interaction between central metal atom/ion and ligand is electrostatic in nature. In free metal ions, the five d-orbitals are degenerate. However, in a ligand field e.g., tetrahedral, octahedral, square planar, square pyramidal, trigonal bipyramidal, the degeneracy of 5d-orbitals is lost.
If lobes of d-orbitals of central metal atom/ion are along the axes through which ligands are approaching, the energy of corresponding d-orbital is raised more than the d-orbitals having lobes between teh axes. e.g., octahedral complexes, square planar complexes, square pyramidal compexes.
Which of the following orbitals has the highest energy in square pyramidal ligand field ?View SolutionWhen degenerate d-orbitals of an isolated atom/ion come under influence of magnetic field of ligands, the degeneray is lost. The two set t2g(dxy,dyz,dxz)andeg(dx2−dx2−y2 are either stabilized or destabilized depending upon the nature of magnetic field. it can be expressed diagrammatically as:

Value of CFSE depends upon nature of ligand and a spectrochemical series has been made experimentally, for tetrahedral complexes, Δ is about 4/9 times to Δ0 (CFSE for octahedral complex). this energy lies in visible region and i.e., why electronic transition are responsible for colour. such transition are not possible with d0andd10 configuration.
Q. For an octahedral complex, which of the followin d-electron configuration will give maximum CFSE?View SolutionAccording to V.B.T., atoms of element form bond only to pair up their unpaired electrons present in ground state or excited state. This pairing of unpaired electron will take place by overlapping of orbitals each one having one unpaired electron with opposite spin.
Which of the following combination of orbitals does not from any type of covalent bond (if z-axis is molecular axis)?View SolutionIn case of octahedral compex, if the eg orbitals (dx2−y2 and dz2) are asymmetricaaly filled, their degeneracy is destroyed and the ligands approaching along +Z and −Z directions experiences different amount of repulsions than the ligands approaching along the +X,−X,+Y and −Y directions. As a result, the symmetrical nature of such complexes is lost and either elongation or compression along Z-axis taken place. Answer the following three questions based on the above situation.
In which of the following case, no such elongation or compressions are expected ?View SolutionThe hybrid orbital is obtained by mixing of atomic orbitals of comparable energy.
For which of the following sets of geometry, both axial and equatorial positions are present?View Solution

