Let a random variable X have a binomial distribution with mean 8 and variance 4. If , then is equal to __________.
Video Solution
Text Solution
The correct Answer is:9
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
Let a random variable X have a binomial distribution with mean 8 and variance 4. If P(X≤2)=k216, then k is equal to
A17B121C1D137 - Question 2 - Select One
Let a random variable X have a binomial distribution with mean 8 and variance 4. If P(X≤2)=k216, then k is equal to :
A17B121C1D137 - Question 3 - Select One
A random variable X follows binomial distribution with mean α and variance β. Then,
A0<α<βB0<β<αCα<0<βDβ<0<α
If X be binomial distribution with mean np and variance npq, then find theP(x=k)P(x=k−1).
View SolutionIf X follows binomial distribution with mean 4 and variance 2, find P(|X−4|≤2).
View SolutionA random variable X has the probability distribution given below
Its variance is
 View Solution
View SolutionA random variable X follows Binomial distribution with mean α and variance β. Then,
View SolutionA random variable X has the probability distribution given below
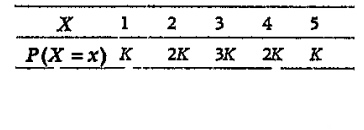
Its variance isView Solution

