A charge 2Q is distributed over three concentric non-conducting spherical shells of radii a, b, c (a < b < c) such that their surface charge densities are equal to one another. The total potential at a point at distance r from their common centre, where r < a , would be:
Q(a+b+c)2πε0(a2+b2+c2)
Q4πε0(a+b+c)
Q12πε0ab+bc+caabc
Q(a2+b2+c2)4πesπ0(a3+b3+c3)
The correct Answer is:A
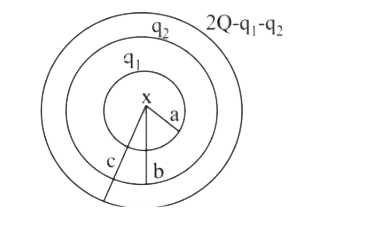
q1a2=q2b2=q3c2=k (constant) →k(a2+b2+c2)=2Q
V(r)=14πε0(q1a+q2b+q3c)
=14πε0(ka+kb+kc)=14πε0×2Q(a2+b2+c2)(a+b+c)
=Q2πesπ0(a+b+ca2+b2+c2)
Similar Questions
A charge Q is distributed over three concentric spherical shells of radii a, b, c (a< b < c) such that their surface charge densities are equal to one another.
The total potential at a point at distance r from their common centre, where r<a, would be :
View SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View Solution
Knowledge Check
A charge q is distributed over two concentric hollow sphere of radii a and b(b>c) such that the surface densities are equal.Find the potential at the common centre.is
AzeroBq4πε0(a+b)(a2+b2)Cq4πε0[1a+1b]Dq4πε0[a+b(a2+b2)]Charges Q,2Q, and −Q are given to three concentric conducting spherical shells A,B and C respectively as shown in figure. The ratio of charge on the inner and outer surface of shell C will be
 A+34B−34C32D−32
A+34B−34C32D−32A conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
AVB2VC4VD−2V
A point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionFigure shows three concentric thin conducting spherical shells A, B and C of radii R, 2R and 3R. The shell B is earthed A and C are given charges q and 2q respectively. Find the charges appearing on all the surface of A,B and C.

[inner surface (A)0,(B)−q,(C)43q
Outer surface (A)q,(B)−43q,(C)23q]
View SolutionThere are two concentric conducting spherical shells of radii 10 cm and 20 cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionA charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
View SolutionThere are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
View Solution
