If circle C passing through the point (2, 2) touches the circle $x^{2} + y^{2} + 4 x - 6 y = 0$ externally at the point (1, 1), then the radius of C is:

A

$\sqrt{12}$

B

$\sqrt{13}$

C

$\sqrt{15}$

D

4

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

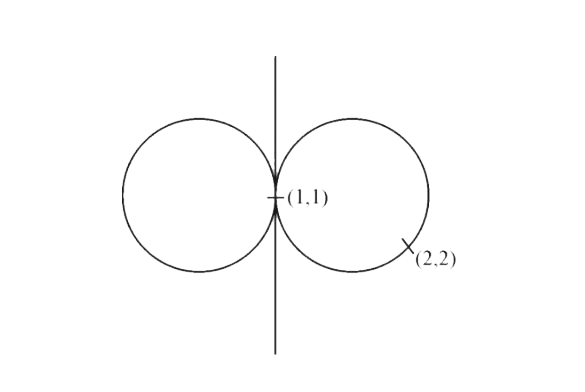
Tangent at (1,1) to $x^{2} + y^{2} + 4 x - 6 y = 0$
$x + y + 2 (x + 1) - 3 (y + 1) = 0$
$3 x - 2 y - 1 = 0$
$S + λ L = 0$ (Family of circle)
$x^{2} + y^{2} + 4 x - 6 y + λ (3 x - 2 y - 1) = 0$
Passes (2,2)
$4 + λ = 0$
$λ = - 4$
Equation of circle : $x^{2} + y^{2} - 8 x + 2 y + 4 = 0$
radius $= \sqrt{16 + 1 - 4} = \sqrt{13}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
Centre of a circle passing through point (0,1) and touching the curve $y = x^{2}$ at $(2, 4)$ is
A $(\frac{16}{5}, \frac{53}{10})$
B $(- \frac{16}{5}, \frac{53}{10})$
C $(- \frac{16}{5}, - \frac{53}{10})$
D $(\frac{16}{5}, - \frac{53}{10})$
Question 2 - Select One
Centre of a circle passing through point (0,1) and touching the curve $y = x^{2}$ at $(2, 4)$ is
A $(\frac{- 16}{5}, \frac{27}{10})$
B $(\frac{- 16}{7}, \frac{5}{10})$
C $(\frac{- 16}{5}, \frac{53}{10})$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile