The sum of all values of θ∈(0,π) satisfying sin22θ+cos42θ=1 is:
A
π
B
3π2
C
5π2
D
None of these
Video Solution
Text Solution
The correct Answer is:B
cos42θ=cos22θ)=0
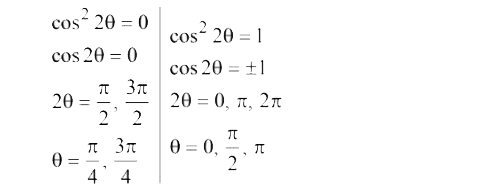
θ∈(0,π)
θ=π4,π2,3π4 ∴ Sum=π4+π2+3π4=6π4=3π2
|
Similar Questions
Knowledge Check
The sum of all values of θ∈(0,π/2) satisfying sin22θ+cos42θ=3/4 is :
AπB5π/4Cπ/2D3π/8The sum of all values of θ∈(0,π2) satisfying sin22θ+cos42θ=34 is
Aπ2BπC3π8D5π4If the sum of all values of θ,0≤θ≤2π satisfying the equation (8cos4θ−3)(cotθ+tanθ−2)(cotθ+tanθ+2)=12 is kπ, then k is equal to :
A2B4C12D8
The sum of all values of θ belonging to [0,π]and satisfying sin3θ=√32 is
View SolutionThe sum of all values of θ belonging to [0,π] and satisfying sin3θ=√32is
View SolutionThe number of values of θ∈[0,2π] that satisfy the equation sin2θ−cosθ=14
View SolutionThe number of values of θ in the range [0,2π] satisfying the equation cos42θ+2sin22θ=17(sinθ+cosθ)8 is
View SolutionThe value of θ , lying between θ=0andθ=π2 and satisfying the equation . ∣∣ ∣ ∣∣1+cos2θsin2θ4sin4θcos2θ1+sin2θ4sin4θcos2θsin2θ1+4sin4θ∣∣ ∣ ∣∣=0,is
View Solution
