Let A=[aij] and B=[bij] be two 4×4 real matrices such that bij=(−2)(i+j−2)aji where i,j=1,2,3,4. If A is scalar matrix of determinant value of 1128 then determinant of B is
64
164
32
none of these
The correct Answer is:C
Given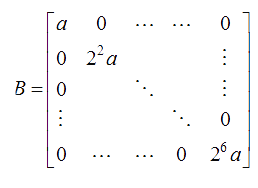 
⇒detB=212a4=212×1128=32
Similar Questions
Let A=[aij] and B=[bij] be two 3×3 real matrices such that bij=(3i+j−2)aji, where i,j=1,2,3. If the determinant of B is 81, then the determinant of A is
View SolutionLet A=[aij]and B=[bij] be two 3×3 real matrices such that bij=(3)(i+j−2)aji ,where i,j=1,2,3 .If the determinant of B is 81 ,then the determinant of A is
View Solution
Knowledge Check
- Question 1 - Select One
Let A=[aij] and B=[bij] be two 3×3 real matrices such that bij=(3)(i+j−2)aji, where i, j = 1,2,3. If the determinant of B is 81, then the determinant of A is :
A1/9B1/81C1/3D3 - Question 2 - Select One
Let A=[aij],B=[bij] are two 3 × 3 matrices such that bij=λi+j−2aij & |B| = 81. Find |A| if λ = 3.
A19B3C181D127 - Question 3 - Select One
Let A=[aij] be a square matrix of order 3 and B=[bij] be a matrix such that bij=2i−jaij for 1≤i,j≤3,∀i,j∈N.
If the determinant of A is same as its order, then the value of ∣∣(BT)−1∣∣ isA13B3C9D127
Let A=[aij] and B=[bij] be two 3×3 real matrices such that bij=(3)(i+j−2)aji ,where i,j=],[1,2,3 .If the determinant of B is 81 ,then the determinant of A is
View SolutionLet A=[aij] and B=[bij] be two 3×3 real matrices such that bij=(3)i+j−2aji, where i,j=1,2,3 .if the determinant of B is 81 ,then the determinant of A is
View SolutionLet A=[aij],B=[bij] are two 3 × 3 matrices such that bij=λi+j−2aij & |B|=81. Find |A| if λ = 3.
View SolutionLet A=[aij] be a square matrix of order 3 and B=[bij] be a matrix such that bij=2i−jaij for 1≤i,j≤3,∀i,j∈N.
If the determinant of A is same as its order, then the value of ∣∣(BT)−1∣∣ isView SolutionLet P=[aij] be a 3×3 matrix and let Q=[bij], where bij=2i+jaij for 1≤i,j≤3. If the determinant of P is 2, then the determinant of the matrix Q is
View Solution