Area of the regin enclosed by the region y2≤3x,x2+y2≤4andy≥0 is:
A
4π−√36
B
4π−√34
C
4π+√36
D
None of these
Text Solution
The correct Answer is:C
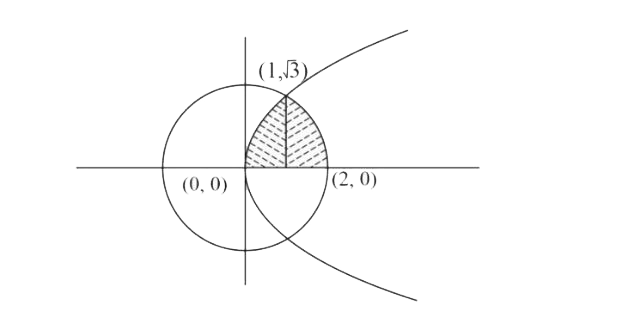
∫10√3√xdxt∫21√4−x2dx
√3⎛⎝x3232⎞⎠1+[x+√4−x22+42sin−1x2]21 ⎡⎢
⎢
⎢
⎢⎣x2+3x−4=0x2+4x−x−4=0x(x+y)−(x+y)=0(x−y)(x+y)=0
2√33+π=√32−π3
√3(23−12)+2π3⇒√36+2π3=4π+√36
|
Similar Questions
Knowledge Check
Area of region enclosed by the region y2≤3x,x2+y2≤4 and y≥0 is :
A4π−√36B4π−√34C4π+√36DNone of theseThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},isAπ−43Bπ−83Cπ−4√23Dπ2−2√23The area (in square units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
Aπ−43Bπ−83Cπ−4√23Dπ2−2√23
The area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
View SolutionCalculate the area enclosed in the region
(i) {(x,y):x2+y2≤1≤x+y}
(ii) {(x,y):x2+y2≤4x,4x2+4y2≤9}
(iii) {(x,y):x2+y2≤16,x2≤6y}
(iv) {(x,y):y2≤6ax,x2+y2≤16a2}
(v) {(x,y):x2+y2≤8,x2≤2y}.
View SolutionThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},is
View SolutionThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},is
View Solution3x+4y≤18,2x+3y≥3andx,y≥0 is
View Solution
