A particle (m = 1kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaches point C (height 1 m), the vertical speed of the particle (in m/s) is (Figure drawn is schematic and not to scale , take g = 9.8 m/sec2) [Take ]
![A particle (m = 1kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaches point C (height 1 m), the vertical speed of the particle (in m/s) is (Figure drawn is schematic and not to scale , take g = 9.8 m/sec^(2)) [Take ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/VMC_JEE_REV_TST_24_E01_023_Q01.png)
The correct Answer is:2.23
mghA=mghc+12mv2
V=√2g(2−1)=v=2√5=2×2.3=4.46m/s
Vy=Vsin30∘
Vy=vsin30∘=4.46×12=2.23m/s
Similar Questions
A particle (m = 3 kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaching its highest point P (height 1.5 m) the kinetic energy of the prarticle (in J) is : Figure drawn is schematic and not to scale , take g = 10ms−2
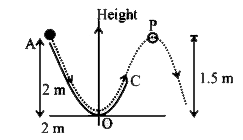
View SolutionA particle (m = 2 kg) slides down a smooth track AOC starting from rest at point A (height = 5m). After reaching point C (height =1m), the particle continues to move freely in air as a projectile. The particle velocity at point C is at angle 60∘ with the horizontal. The maximum height attained by particle after leaving point C is _____(in m). [figure drawn is schematic and hot to scale : take =ms−2]
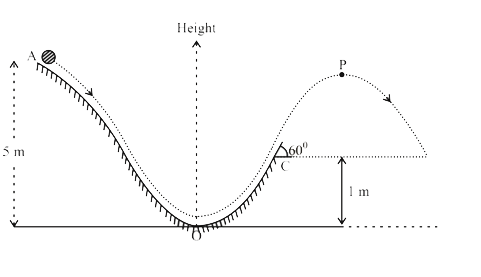
View Solution
Knowledge Check
A particle slides down a frictionless paraboli (y=x2) track (A−B−C) starting from rest at point A.Point B is at the vertex of parabola and point C is at a height less than that of point A.After C,the particle moves freely in air as a projectile. If the particle reaches highest point at P,then
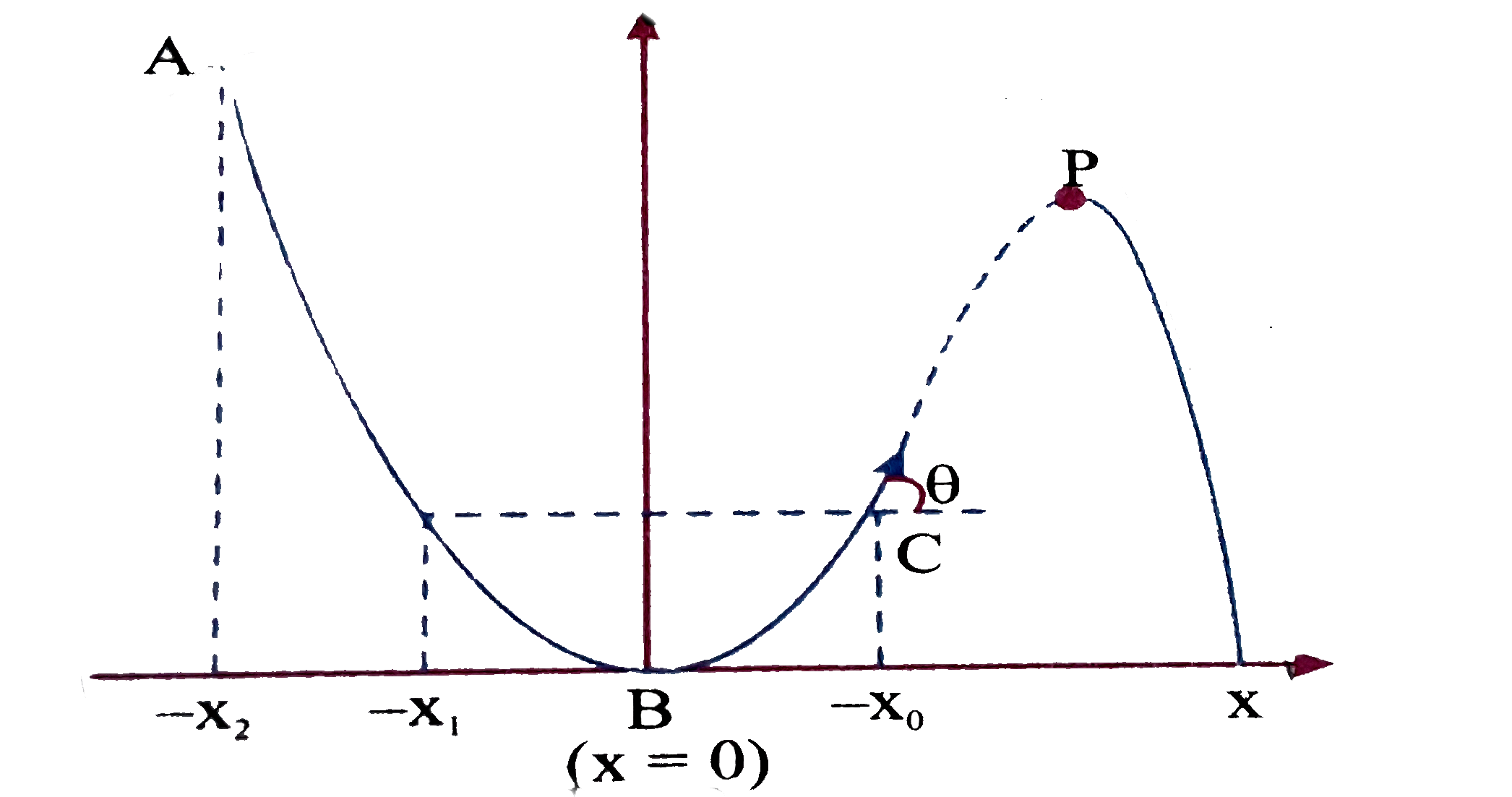AKE at P=KE at BBheight at P=height at ACtotal energy at P=total energy at ADtime of travel from A to B =time of travel from B to PA particle (m=1kg) slides down in frictionless-track AOC starting from rest at a point A(height 2m). After reaching on horizontal smooth track compresses a light spring of spring constant K= 100N/m, by distance 0.5 m before coming to rest. The height (in m) of horizontal track is.........(Take g=10m/s2)
A0.65B1C0.75D1.75A particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is
A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these
A particle moves in east direction with 15m/sec for 2 sec then moves in northward with 5 m/s for 8 sec. A average speed of the particle is :-
View SolutionA block shown in figure -3.12 slides on a semicircular frictionless track. If it starts from rest at position A, what is its speed at the point marked B ? Take g=10m/s2
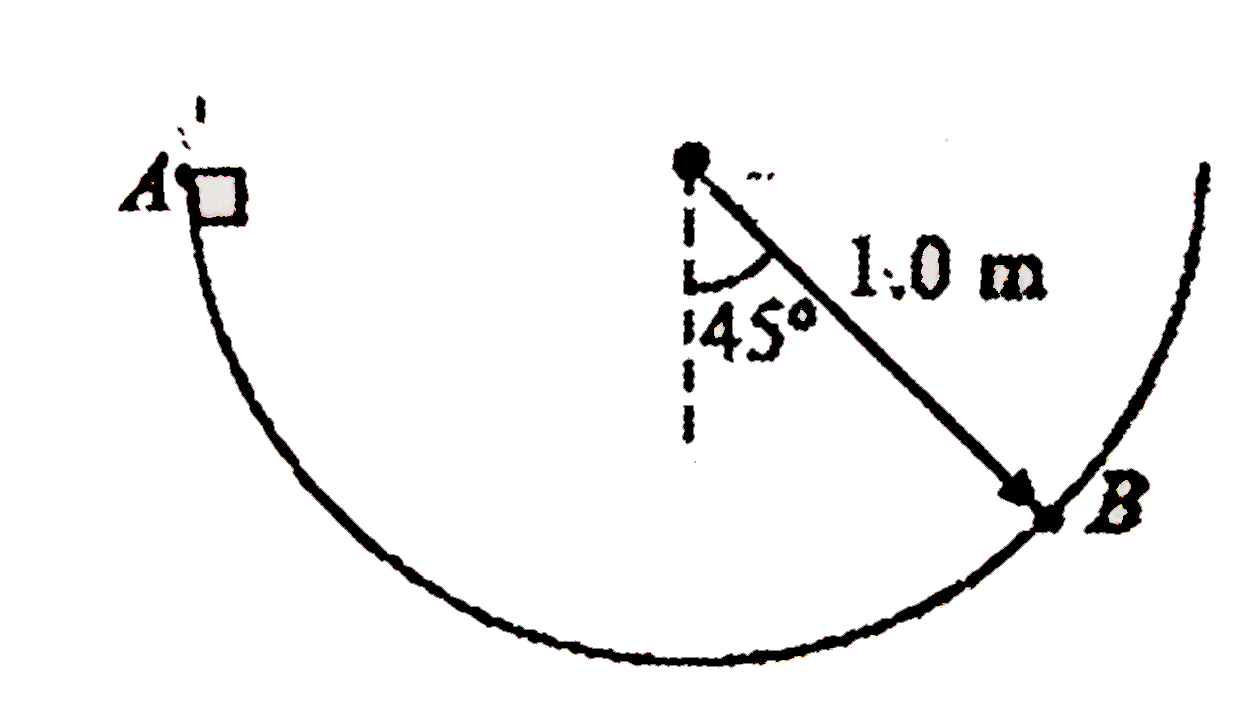
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
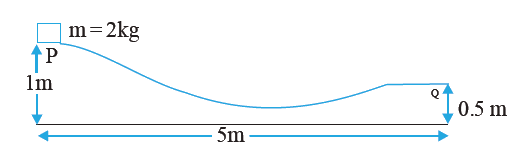
View SolutionA particle of mass m is released from rest from a point A of a wedge of mass 4m free to slide on a frictionless horizontal plane.The particle slides down the smooth face AB of the wedge.When the velocity of the wedge is 0.2m/s the velocity of the particle in m/s relative to the wedge is
View SolutionA particle of mass m is released from rest from a point A of a wedge of mass 4m free to slide on a frictionless horizontal plane. The particle slides down the smooth face AB of the wedge. When the velocity of the wedge is 0.2 m/s the velocity of the particle in m/s relative to the wedge is
View Solution