Question

Consider the parabola $y^2=8x$. Let ${△}_1$ be the area of the triangle formed by the endpoints of its latus rectum and the point P$(\frac{1}{2},2)$ on the parabola, and ${△}_2$ be the area of the triangle formed by drawing tangents at P and at the endpoints of the latus rectum. Then is $\frac{{\Delta }_1}{{\Delta }_2}$ is.

Explanation

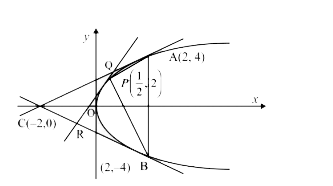
`y^(2) = 8x`
Tangents at the endpoints of latus rectum meet the directrix on the x - axis at (-2 , 0)
`Delta_(1)` = Area of `DeltaABQ = (1)/(2)(8) (2 - (1)/(2)) = 6 , Delta_(2)` = Area of `Delta CQR`
Now , tangent at point A (2,4) is 4y = 4(x + 2) or y = x + 2
Also , tangent at point `P((1)/(2) ,2) is 2y = 4 (x + (1)/(2))` or y = 2x + 1
Solving for Q and R , we get Q (1, 3) and R (-1,-1)
Hence , area of `DeltaCQR is (1)/(2) |{:(-1 ,-1, 1),(1,3,1),(-2,0,1):}| = (1)/(2) (-3 + 2 + 6 + 1) = 3
Hence , the ratio of area is `(6)/(3) = 2.`