If $q_{1},_{2}, q_{3}$ are roots of the equation $x^{3} + 64 = 0$ , then the value of $∣ ∣ ∣ ∣ ∣ \begin{matrix} q_{1} & q_{2} & q_{3} q_{2} & q_{3} & q_{1} q_{3} & q_{1} & q_{2} \end{matrix} ∣ ∣ ∣ ∣ ∣$ is :-

A

1

B

4

C

16

D

0

Text Solution

Verified by Experts

The correct Answer is:D

$∣ ∣ ∣ ∣ ∣ \begin{matrix} q_{1} & q_{2} & q_{3} q_{2} & q_{3} & q_{1} q_{3} & q_{1} & q_{2} \end{matrix} ∣ ∣ ∣ ∣ ∣ \to C_{1} + C_{2} + C_{3}$
$= (q_{1} + q_{2} + q_{3}) ∣ ∣ ∣ ∣ ∣ \begin{matrix} 1 & q_{2} & q_{3} 1 & q_{3} & q_{1} 1 & q_{1} & q_{2} \end{matrix} ∣ ∣ ∣ ∣ ∣$
$= 0 (∵ sum of roots is zero)$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
If $q_{1}, q_{2}, q_{3}$ ar rootsof the equation $x^{3} + 64 = 0$ then value of $∣ ∣ ∣ ∣ ∣ \begin{matrix} q_{1} & q_{2} & q_{3} q_{2} & q_{3} & q_{1} q_{3} & q_{1} & q_{2} \end{matrix} ∣ ∣ ∣ ∣ ∣$
A1
B4
C16
D0
Question 2 - Select One
If the lines $p_{1} x + q_{1} y = 1 + q_{2} y = 1 and p_{3} x + q_{3} y = 1$ be concurrent, show that the point $(p_{1}, q_{1}), (p_{2}, q_{2}) and (p_{3}, q_{3})$ are collinear.
Aare collinear
Bform an equilateral triangle
Cform a scalene triangle
Dform a right angled triangle
Question 3 - Select One or More
In, the charges on $C_{1}, C_{2}$ , and $C_{3}$ , are $Q_{1}, Q_{2}$ , and $Q_{3}$ , respectively.
.
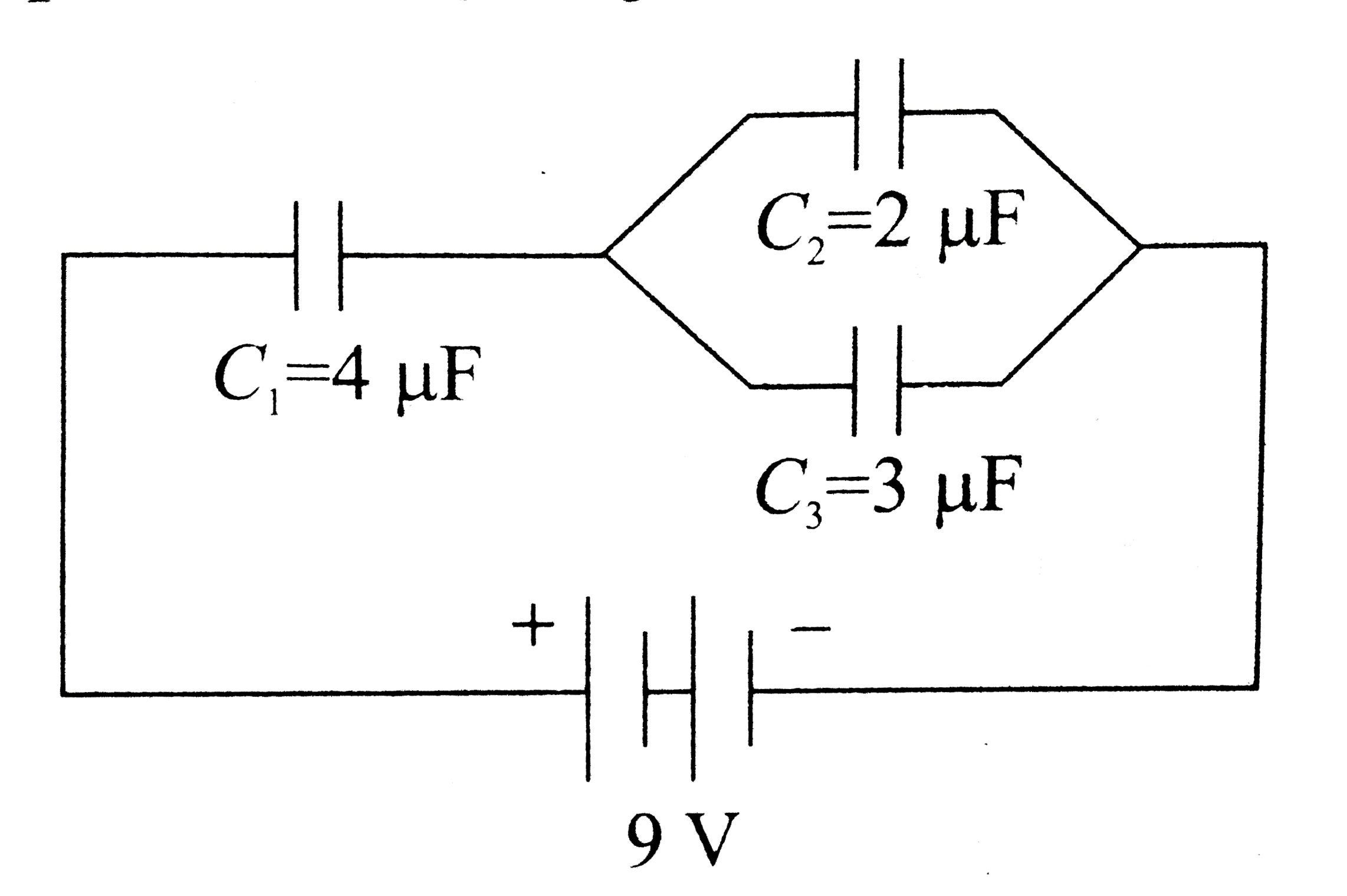A $Q_{2} = 8 μ C$
B $Q_{3} = 12 μ C$
C $Q_{1} = 20 μ C$
D $Q_{2} = 12 μ C$

Recommended Questions

Home
Ask Doubt
Profile