A biased coin with probability of getting head is twice that of tail, is tossed 4 times If a random variable X is number of heads obtained, then expected value of X is :

A

$\frac{2}{3}$

B

$\frac{8}{3}$

C

$2$

D

$\frac{16}{3}$

Text Solution

Verified by Experts

The correct Answer is:B

Let X is number of heads obtained
$p = \frac{2}{3}$ probability of getting head
$q = \frac{1}{3}$ probability of getting tail.

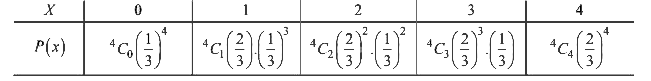
$E (x) = S u m ξ π$
$= 0 \frac{1}{3^{4}} + 1 \times \frac{8}{3^{4}} + 2 x \frac{24}{3^{4}} + 4 \times \frac{16}{3^{4}} = \frac{216}{81} = \frac{8}{3}$ $E (x) = \frac{8}{3}$ .

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
Un biased coin is tossed 6 times. The probability of getting atmost 4 heads is
A $\frac{7}{64}$
B $\frac{57}{64}$
C $\frac{21}{32}$
D $\frac{11}{32}$
Question 2 - Select One
A coin is tossed three times. The probability of getting head and tail alternately, is
A $1 / 8$
B $1 / 2$
C $1 / 4$
Dnone of these
Question 3 - Select One
A coin is tossed three times. What is the probability of getting head and tail (HTH) or tail and head (THT) alternatively ?
A $\frac{1}{8}$
B $\frac{1}{4}$
C $\frac{1}{2}$
D $\frac{3}{4}$

Recommended Questions

Home
Ask Doubt
Profile