If $cos θ = \frac{cos α - cos β}{1 - sin α sin β}$ , prove that one value of $t a n \frac{θ}{2} = \frac{t a n \frac{α}{2} - t a n \frac{β}{2}}{1 - t a n \frac{α}{2} - t a n \frac{β}{2}}$

Video Solution

Text Solution

Verified by Experts

$cos θ = \frac{cos α - cos β}{1 - cos α cos β}$

or, $\frac{1 - {tan}^{2} \frac{θ}{2}}{1 + {tan}^{2} \frac{θ}{2}} = \frac{cos α - cos β}{1 - cos α cos β}$

or, $\frac{1 + {tan}^{2} \frac{θ}{2}}{1 - {tan}^{2} \frac{θ}{2}} = \frac{1 - cos α cos β}{cos α - cos β}$
or $t a n \frac{θ}{2} = \frac{t a n \frac{α}{2} - t a n \frac{β}{2}}{1 - t a n \frac{α}{2} - t a n \frac{β}{2}}$ or, ${tan}^{2} \frac{θ}{2} = \frac{1 - cos α cos β - cos α + cos β}{1 - cos α cos β + cos α - cos β}$

or, ${tan}^{2} \frac{θ}{2} = \frac{(1 - cos α) (1 + cos β)}{(1 + cos α) (1 - cos β)}$

or, ${tan}^{2} \frac{θ}{2} = tan 2 \frac{α}{2} {cos}^{2} \frac{β}{2}$

or, ${tan}^{2} \frac{θ}{2} = \pm tan \frac{α}{2} cot \frac{β}{2}$
$t a n \frac{θ}{2} = \frac{t a n \frac{α}{2} - t a n \frac{β}{2}}{1 - t a n \frac{α}{2} - t a n \frac{β}{2}}$

Updated on:21/07/2023

The least value of $g (t) = 8 t - t^{4}$ on [-2, 1] is
A $- 16$
B $- 20$
C $- 32$
D7
The minimum value of the expression ${(t^{2} + 1 - α)}^{2} + {(2 t - α - 4)}^{2}$ is $(t, α \in R)$
A2
B3
C8
D10
The block is in equilibrium

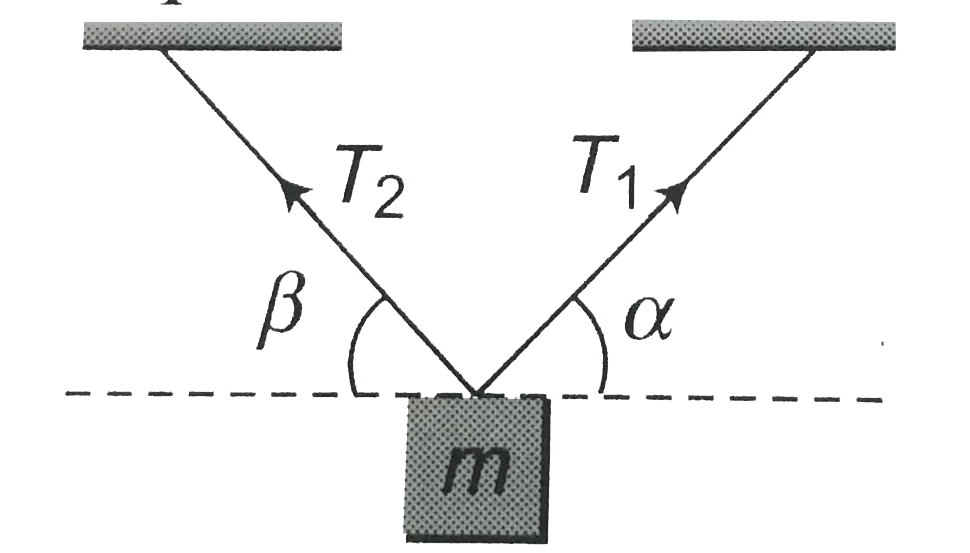
$(i) T_{1} = \frac{m g cos β}{sin (α + β)} (i i) T_{2} = \frac{m g cos α}{sin (α + β)}$
$(i i i) \frac{T_{1}}{T_{2}} = \frac{cos β}{cos α} (i v) \frac{T_{1}}{T_{2}} = \frac{cos α}{cos β}$
A(i),(ii)
B(i),(ii),(iii)
C(ii),(iii)
D(iii),(iv)