Question

Two towers AB and CD are situated a distance d apart as shown in Fig. 5.45. AB is 20m high and

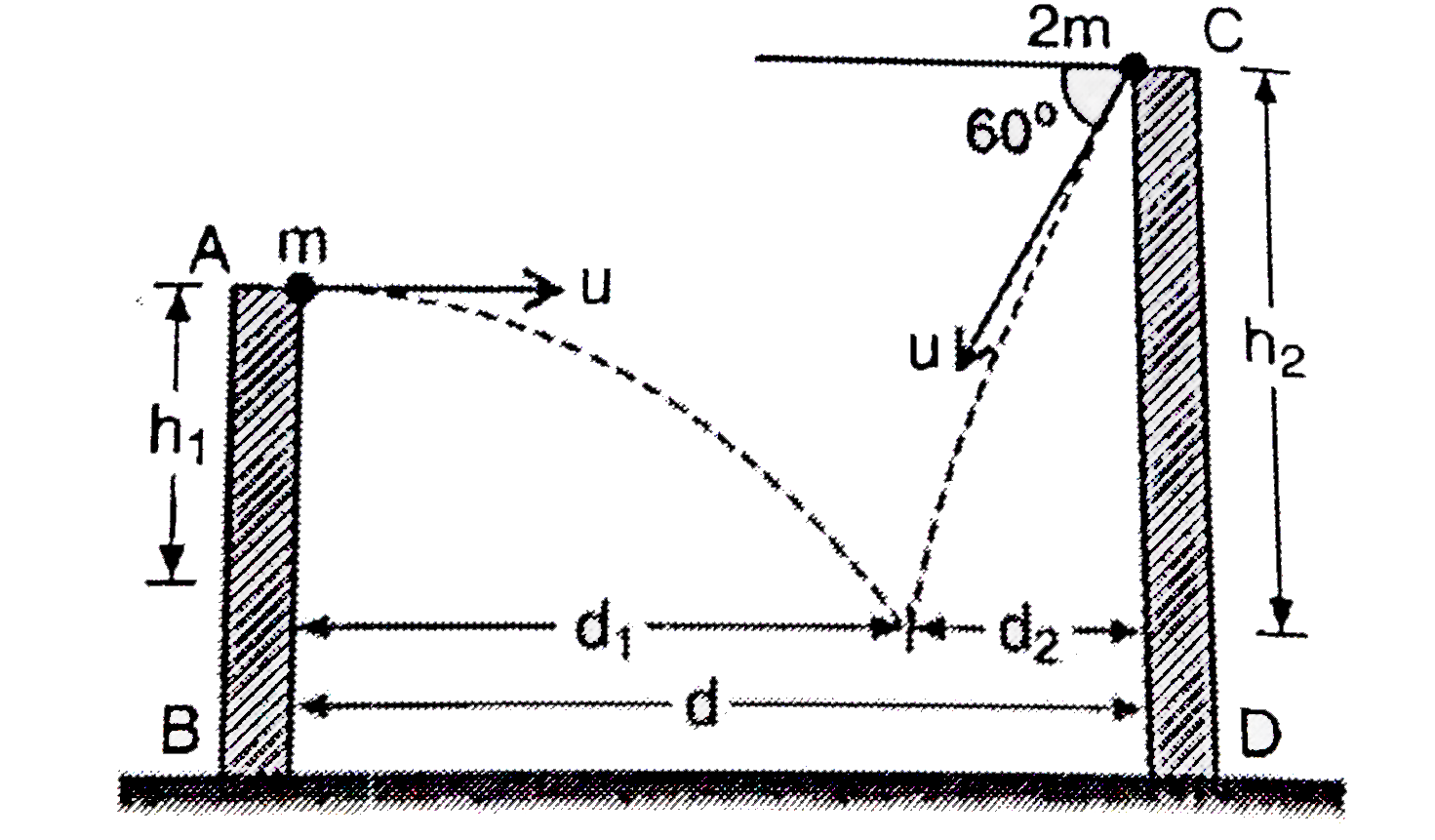
CD is 30m highfrom the ground . An object of mass m is thrown from the top of AB horizontally with a velocity 10m/s towards CD. simu ltaneously another object of mass 2 m is thrown from the top of CD at an angle of ${60}^{\circ }$ to the horizotnal towards AB with the same magnitude of initial velocity as that of the first object. the two objects move in the same vertical plane, clollide in mid air and stick to each other, (a) Calcu late the distance d between the towers and (b) fin the position where the objects hit the ground.

Explanation

Let the two particles collide after time r, then from 2nd equation of motion, i.e.,
`s=ut+(1)/(2)at^(2)`
for vertical motion of A,
`h_(1)=(1)/(2)g t^(2)` ........(i) ltbr. While for B,
`h_(2)=(u sin 60^(@))t+(1)/(2)g t^(@)` ..........(ii)
But as the collision will take place at same level,
`30-h_(2)=20-h_(1),,i.e., h_(2)-h_(1)=10`
Which, in the light of Eqns. (i) and (ii), gives
`10xx((sqrt(3))/(2))t=10, i.e.,t=(2)/sqrt(3)s`
(a) Now as horizontal motion is independent of vertical motion, so from 2nd Eqn. of motion. i.e. s=ut+(1/2)`at^(2)` distance travelled by m towards 2m horizotnall.
`d_(t)=10xx(2)/sqrt(3)=(20)/sqrt(3)m`
and distance travelled by 2m towards m horizontally,
`d_(2)=u cos thetaxxt`
`=10xx(1)/(2)xx(2)/sqrt(3)=(10)/sqrt(3)m`.
So, distance between the towers AB and CD,
`d=d_(1)+d_(@)=(20)/sqrt(3)=(30)/sqrt(3)=10sqrt(3)=17 m`
(b) Applying conservation of linear momentum along horizontal direction
`mu-2mu cos 60^(@)=3mV`, i.e., V=0
i.e., the velocity of combined mass fter collision along horizontal is zero, so after collision it will move vertically down from the point of collision and will hit the ground at a distance `d_(1)=20//sqrt(3)` from AB or at a distance `d_(2)=10//sqrt(3)` from CD between BD.