The displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward quarter revolution where perimeter of the wheel is 4πm, is (Assume the forward direction as x-axis)
√(π+2)∘+4alongtan−1(2)π with x-axis
√(π−2)2+4alongtan−1(2)π−2 with x-axis
√(π−2)2+4 along tan−1(2)π with x-axis
√(π+2)2+4 along tan−1(2)π−2 with x-axis
The correct Answer is:b
S=√y2+x2 and θ=tan−1(yx)
Topper's Solved these Questions
Similar Questions
What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution? Take the radius of the wheel as R and the x-axis as the forward direction?
View SolutionA wheel of circumference C is at rest on the ground. When the wheel rolls forward through half a revolution, then the displacement of initial point of contact will be
View Solution
Knowledge Check
- Question 1 - Select One
Assertion : The total displacement moved by a point located on the periphery of a wheel of radius R in one revolution is 2πR. Wheel is rolling.
Reason : In rolling motion of a wheel, every point on its periphery comes in contact with the surface once in one revolution.ABoth Assertion & Reason are true & the Reason is a correct explanation of the Assertion.BBoth Assertion and Reason are true but Reason is not a correct explanation of the Assertion.CAssertion is true but the Reason is false.DBoth Assertion & Reason are false. - Question 2 - Select One
A wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
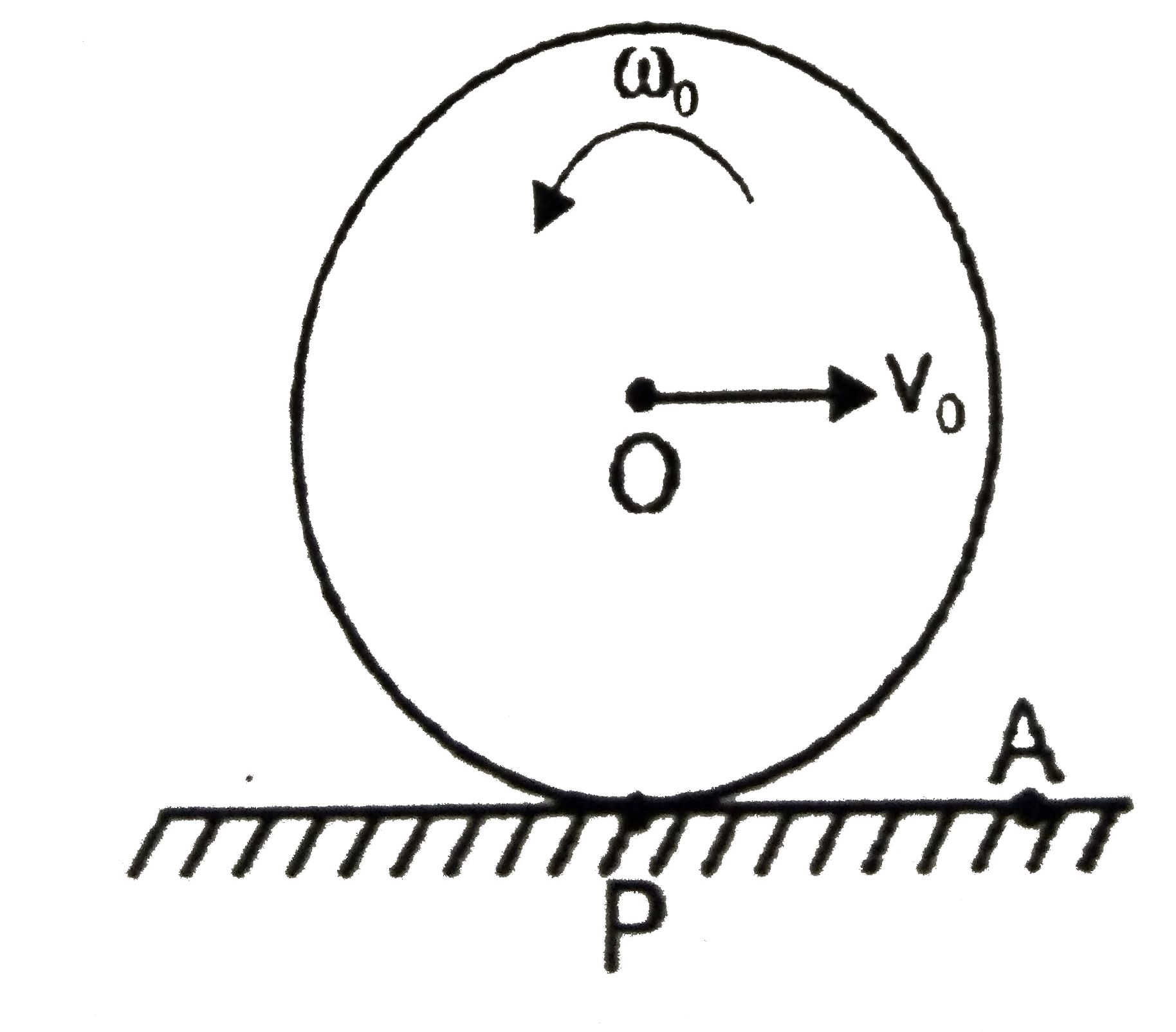
If above question , distance travelled by centre of mass of the wheel before it stops is −Av202μg(1+r2k2)Bv202μgCv202μg(1+k2r2)DNone of these - Question 3 - Select One
A wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
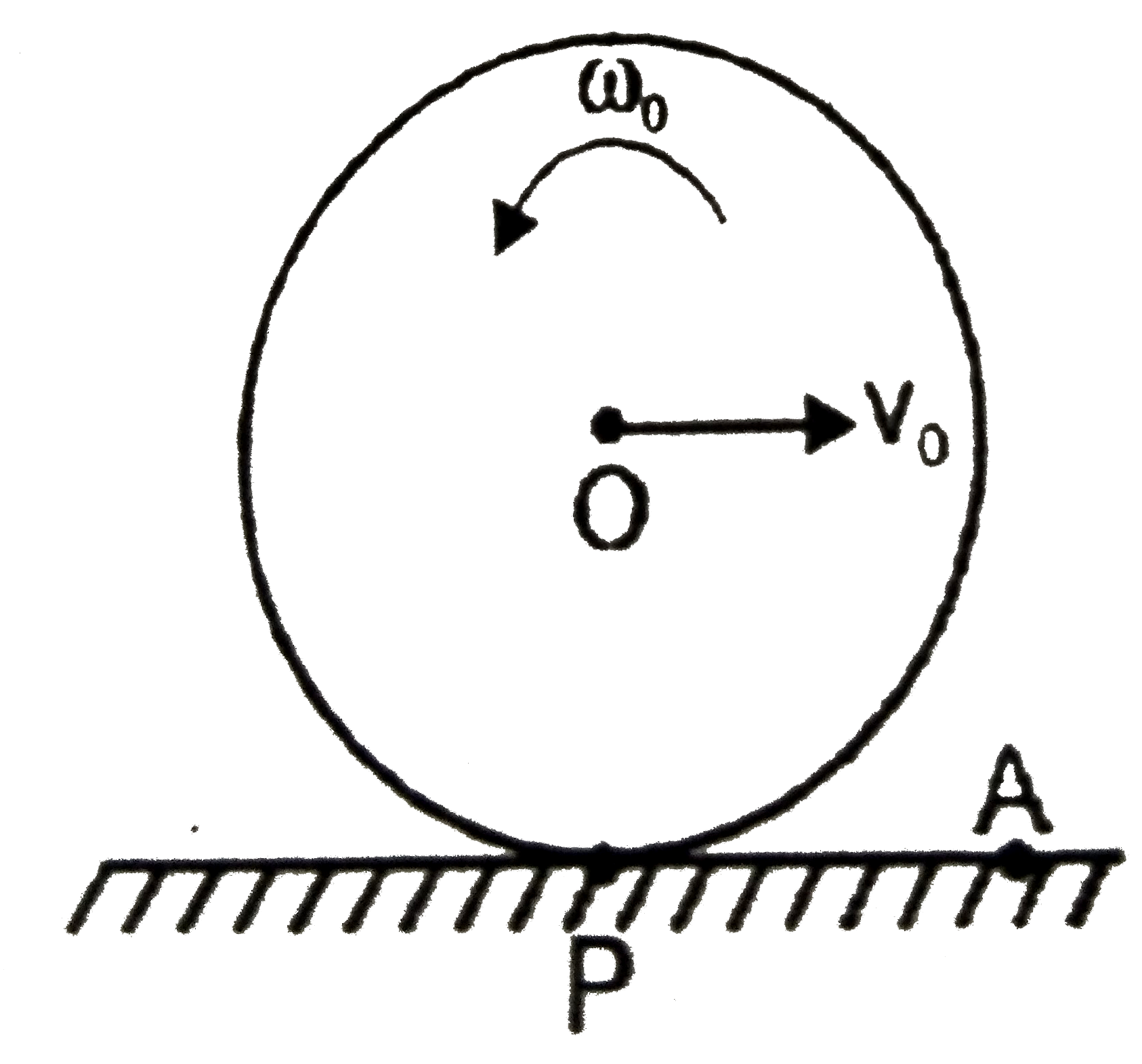
If the wheel comes to permanent rest after sometimes, then :Av0=ω0rBv0=ω0k2rCv0=ω0r2RDV0=ω0(r+k2r)
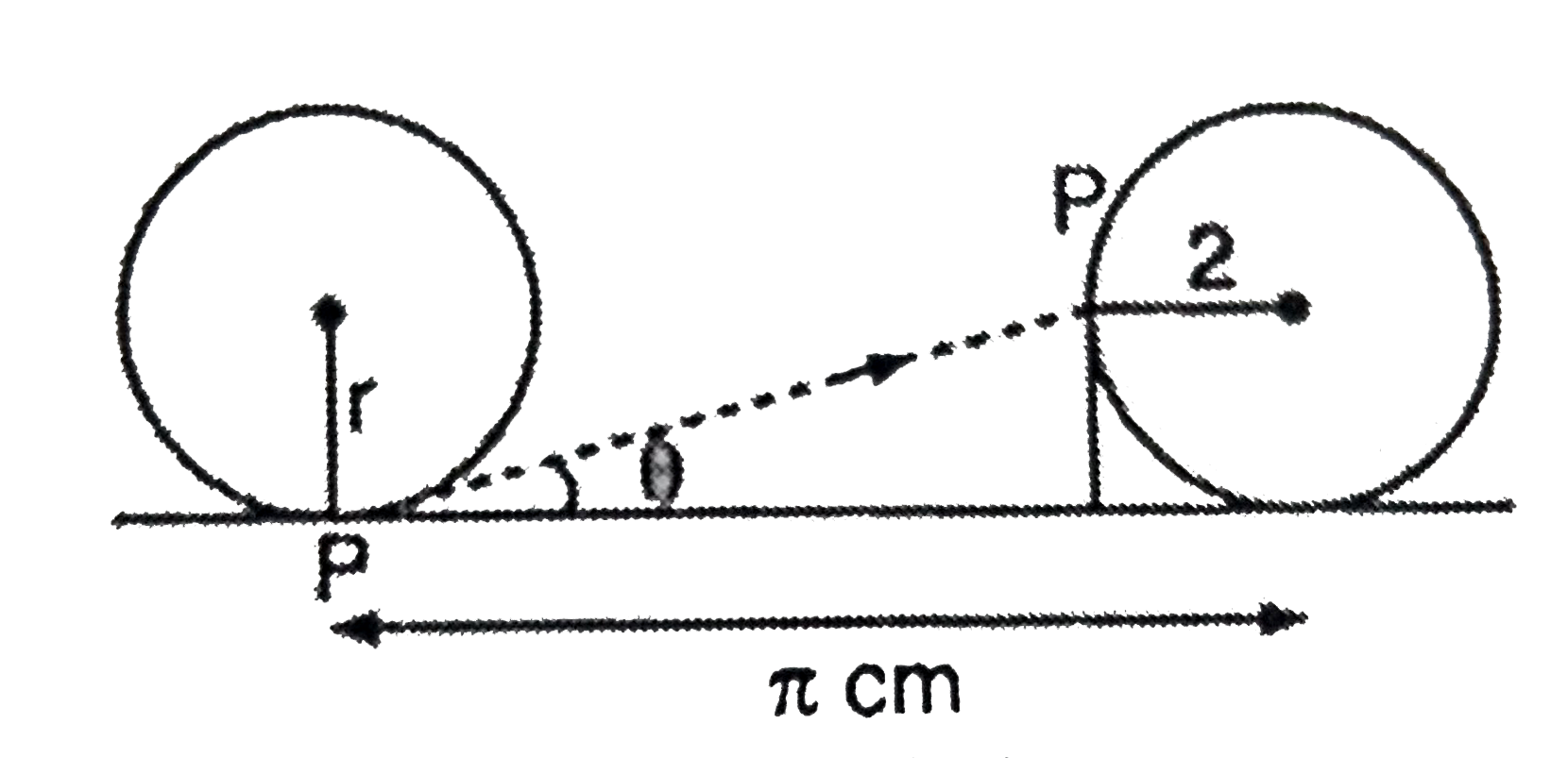
If a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be
 View Solution
View SolutionThe fore wheel of a carriage makes 6 revolutions more than the rear wheel in going 120m. If the diameter of the fore wheel be increased by 14 its present diameter and the diameter of the rear wheel be increased by one-fifth of its present diameter, then the fore wheel makes 4 revolutions more than the rear wheel in going the same distance. Find the circumference of each wheel of the carriage.
View SolutionFigure shows a student, sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose moment of inertia is I about its central axis. The wheel is rotating at an angular speed ωi from an overead perspective, the rotation is counter clockwise. The axis of the wheel point vertical, and the angular momentum →Li of the wheel points vertically upward. The student now inverts the wheel, as a result, the student and stool rotate about the stool axis. With what angular speed and direction does the student then rotate? (The moment of inertia of the student+stool+wheel system about the stool axis is I0)
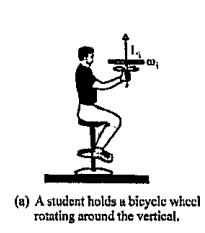
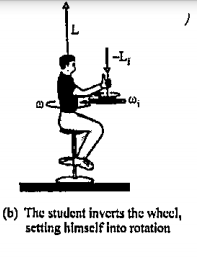 View Solution
View SolutionThe square of angular velocity ω of a certain wheel increases linearly with the angular displacement θ during 100 revolutions of the wheel's motion as shown in the figure. The time t required for given 100 revolutions is 10mπn. Find (m+n).
'(##CEN_KSR_PHY_JEE_C07_028_Q17##)'View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
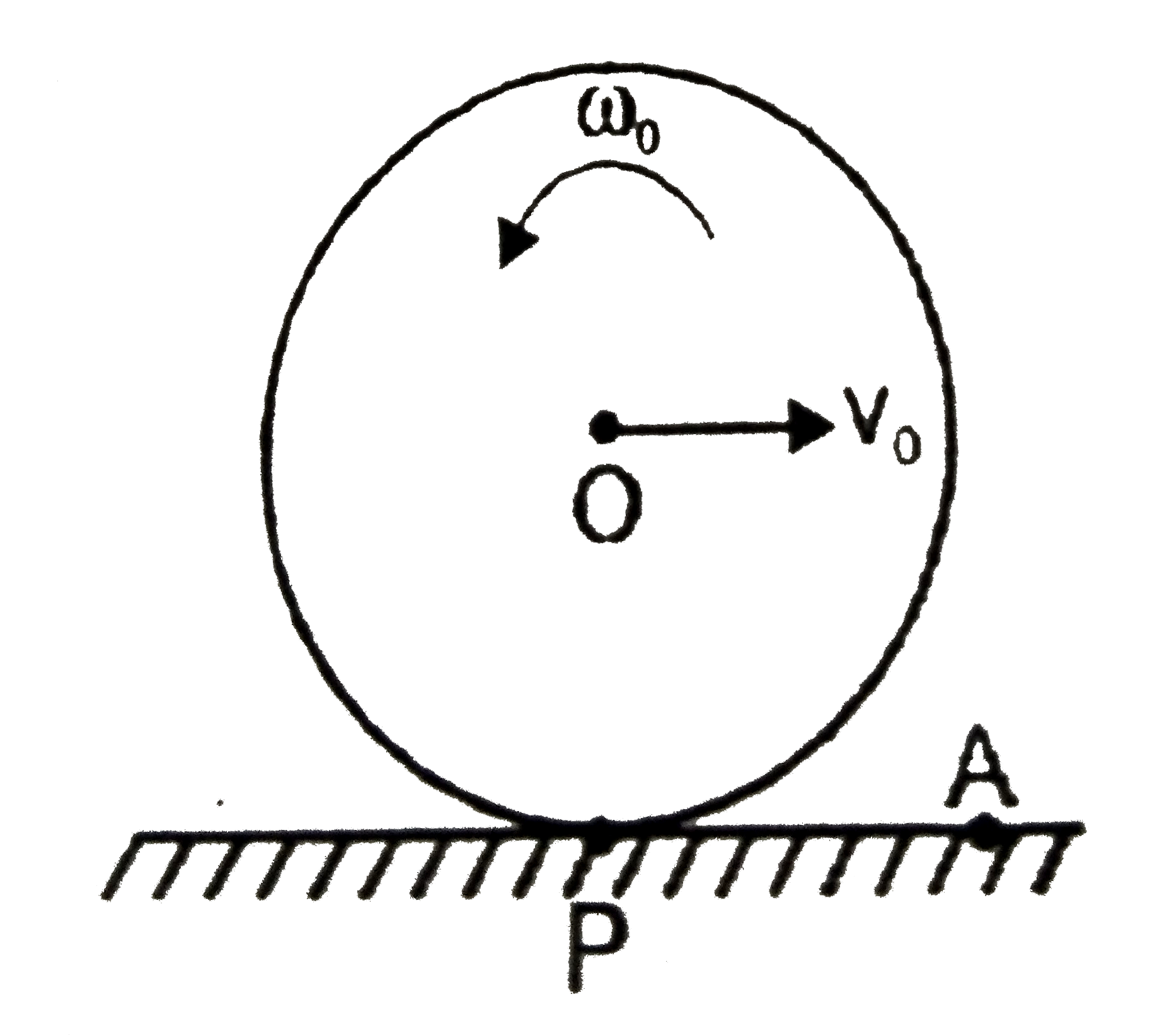
Which of the following is conserved ?View Solution

